Question

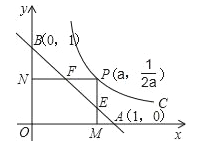
【题目】甲、乙两车分别从两地同时出发，甲车匀速前往地，到达地立即以另一速度按原路匀速返回到地；乙车匀速前往地，设甲、乙两车距地的路程为(千米)，甲车行驶的时间为(小时)与之间的函数图象如图所示：

（1）甲车从地开往地时的速度是_________；乙车从地开往地时的速度是______.

（2）图中点的坐标是(______，______)；

（3）求甲车返回时与之间的函数关系式，并写出自变量的取值范围.

Answer 1

【答案】（1）千米/时，千米/时；（2）2.5,300；（3）.

【解析】

（1）根据题意列算式即可得到结论；
（2）根据甲车从A地开往B地时的速度即可得出点P的坐标；
（3）利用待定系数法求解即可．

解：(1)甲车从A地开往B地时的速度是：180÷1.5=120千米/时，乙车从B地开往A地的速度是：（300-180）÷1.5=80千米/时，
故答案为：120千米/时；80千米/时；

（2）P的横坐标是：300÷120=2.5，
∴点P的坐标为（2.5，300）．
故答案为：（2.5，300）；

(3)设甲车返回时与之间的函数关系式为，又

，解得，

∴甲车返回时与之间的函数关系式为