��Ŀ����
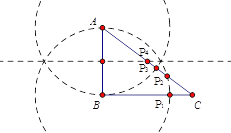
����Ŀ����ͼ����Rt��ABC�У���B=Rt��,ֱ�DZ�AB��BC�ij�(AB��BC)�Ƿ���![]() 2��7
2��7![]() ��12��0������������P�ӵ�A��������ÿ��1����λ���ٶ�����ABC�� A��B��C��A�ķ����˶����˶�ʱ��Ϊt(��)��
��12��0������������P�ӵ�A��������ÿ��1����λ���ٶ�����ABC�� A��B��C��A�ķ����˶����˶�ʱ��Ϊt(��)��
��1����AB��BC�ij���
��2������P�˶�����BC��ʱ�������ʹAP��Ϊ![]() ʱ�˶�ʱ��t��ֵ��
ʱ�˶�ʱ��t��ֵ��
��3����P���˶��Ĺ��������Ƿ���ڵ�P��ʹ��ABP�ǵ��������Σ������ڣ�������˶�ʱ��t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��AB��3��BC��4��2��t��4ʱ��AP��![]() ��3����tΪ9���9.5���6 (��)��
��3����tΪ9���9.5���6 (��)��![]() (��)ʱ����ABP�ǵ���������.
(��)ʱ����ABP�ǵ���������.
�������������������1���ⷽ��x2��7x��12��0 ���ɵ�AB��BC�ij���
��2���ɡ�ABP��ֱ�������θ��ݹ��ɶ����ɵõ�BP�ij����Ӷ��õ��˶���ʱ�䣻
��3���ֱ���A��BΪԲ�ģ���AB��Ϊ�뾶��Բ��Բ��BC��AC�Ľ��㼴Ϊ�����P�㣬����AB���д��ߣ��д�����AC�Ľ���Ҳ�������P�㣬�Ӷ��ɵ��˶�ʱ��.
�����������1����x2��7x��12��(x��3)(x��4)��0
��![]() ��3��
��3��![]() ��4��
��4��
��AB��3��BC��4
��2���������![]()
��![]() ��
�� ![]() (��ȥ)
(��ȥ)
��t��4ʱ��AP��![]()
��3�����ڵ�P��ʹ��ABP�ǵ���������.
����AP��AB��3ʱ�� t=9(��).
����BP��BA��3ʱ����p��AC��ʱ�� t=![]() (��)
(��)
��p��BC��ʱ�� t=6(��)
����BP=AP (��PΪAC�е�ʱ)��
��t��9.5(��)
��֪��tΪ9���9.5���6 (��)��![]() (��)ʱ����ABP�ǵ���������.
(��)ʱ����ABP�ǵ���������.