题目内容
【题目】在正方形ABCD中,BD是一条对角线,点P在CD上(与点C,D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QM⊥BD于M,连接AM,PM(如图1).

(1)判断AM与PM的数量关系与位置关系并加以证明;
(2)若点P在线段CD的延长线上,其它条件不变(如图2),(1)中的结论是否仍成立?请说明理由.
【答案】(1)AM=PM,AM⊥PM.(2)成立,理由见解析.
【解析】
试题分析:(1)先判断出△DMQ是等腰直角三角形,再判断出△MDP≌△MQC(SAS),最后进行简单的计算即可;
(2)先判断出△DMQ是等腰直角三角形,再判断出△MDP≌△MQC(SAS),最后进行简单的计算即可.
试题解析:(1)连接CM,

∵四边形ABCD是正方形,QM⊥BD,
∴∠MDQ=45°,
∴△DMQ是等腰直角三角形.
∵DP=CQ,
在△MDP与△MQC中

∴△MDP≌△MQC(SAS),
∴PM=CM,∠MPC=∠MCP.
∵BD是正方形ABCD的对称轴,
∴AM=CM,∠DAM=∠MCP,
∴∠AMP=180°-∠ADP=90°,
∴AM=PM,AM⊥PM.
(2)成立,
理由如下:
连接CM,
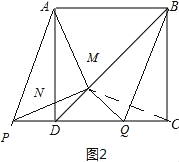
∵四边形ABCD是正方形,QM⊥BD,
∴∠MDQ=45°,
∴△DMQ是等腰直角三角形.
∵DP=CQ,
在△MDP与△MQC中

∴△MDP≌△MQC(SAS),
∴PM=CM,∠MPC=∠MCP.
∵BD是正方形ABCD的对称轴,
∴AM=CM,∠DAM=∠MCP,
∴∠DAM=∠MPC,
∵∠PND=∠ANM
∴∠AMP=∠ADP=90°
∴AM=PM,AM⊥PM.

练习册系列答案
相关题目