题目内容
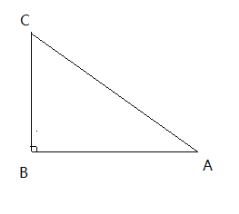
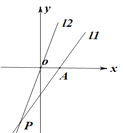
【题目】在直角坐标系中,直线![]() 经过点(2,3)和(-1,-3),直线
经过点(2,3)和(-1,-3),直线![]() 经过原点,且与直线
经过原点,且与直线![]() 交于点P(-2,a).
交于点P(-2,a).
(1)求a的值.
(2)(-2,a)可看成怎样的二元一次方程组的解?
(3)设直线![]() 与x轴交于点A,你能求出△APO的面积吗?
与x轴交于点A,你能求出△APO的面积吗?
【答案】(1)a=-5;(2)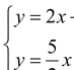 ;(3)
;(3)![]() .
.
【解析】试题分析:(1)首先利用待定系数法求得直线的解析式,然后直接把P点坐标代入可求出a的值;
(2)利用待定系数法确定L2得解析式,由于P(-2,a)是L1与L2的交点,所以点(-2,-5)可以看作是解二元一次方程组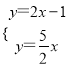 所得;
所得;
(3)先确定A点坐标,然后根据三角形面积公式计算;
试题解析:
(1)解:设![]() :
: ![]() 过(2,3)和(-1,-3)
过(2,3)和(-1,-3)
∴![]()
∴k=2;b=-1
∴![]() :y=2x-1,
:y=2x-1,
∵过点P(-2,a)
∴a=-2×2-1=-5
设l2:y=mx且过点P(-2,-5)
∴![]()
∴(-2,a)可看成二元一次方程组 的解;
的解;

(3)直线11与x轴的交点坐标,即当y=0时,x=0.5,
∴A(0.5,0)
∴OA=0.5
∵(-2,a)可看成二元一次方程组 的解,
的解,
∴a=-5,
作PF⊥x轴,
∴PF=5
∴SPOA=![]() .
.

练习册系列答案
相关题目