题目内容
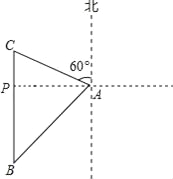
【题目】如图,海中一小岛有一个观测点A,某天上午观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.B处距离观测点30![]() 海里,若该渔船的速度为每小时30海里,问该渔船多长时间到达观测点A的北偏西60°方向上的C处?(计算结果用根号表示,不取近似值)
海里,若该渔船的速度为每小时30海里,问该渔船多长时间到达观测点A的北偏西60°方向上的C处?(计算结果用根号表示,不取近似值)

【答案】该渔船从B处开始航行(1+![]() )小时到达C处.
)小时到达C处.
【解析】
试题分析:过点A作AP⊥BC,垂足为P,在Rt△APB利用三角函数求的AP和PB的长,则在直角△APC中利用三角函数即可求得PC的长,即可求得BC的长,然后根据速度公式求解.
试题解析:过点A作AP⊥BC,垂足为P.
在Rt△APB中,∵∠APB=90°,∠PAB=45°,AB=30![]() ,
,
∴BP=AP=![]() AB=30
AB=30![]() .
.
在Rt△APC中,∵∠APC=90°,∠PAC=30°,
∴tan∠PAC=![]() ,
,
∴CP=APtan∠PAC=30.
∵PC+BP=BC=30+30![]() ,
,
∴航行时间:(30+30![]() )÷30=1+
)÷30=1+![]() (小时).
(小时).
答:该渔船从B处开始航行(1+![]() )小时到达C处.
)小时到达C处.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目