题目内容
如图⑴,一等腰直角三角尺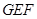 (
(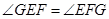 )的两条直角边与正方形
)的两条直角边与正方形 的两条边分别重合在一起. 现正方形
的两条边分别重合在一起. 现正方形 保持不动,将三角尺
保持不动,将三角尺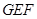 绕斜边
绕斜边 的中点
的中点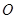 (点
(点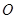 也是
也是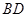 中点)旋转.
中点)旋转.

① 若将三角尺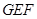 绕斜边
绕斜边 的中点
的中点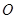 按顺时针方向旋转到如图⑵,当
按顺时针方向旋转到如图⑵,当 与
与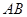 相交于点
相交于点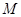 ,
,
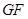 与
与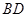 相交于点
相交于点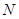 时,通过观察或测量
时,通过观察或测量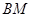 、
、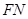 的长度,猜想
的长度,猜想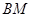 、
、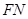 满足的数量关系,并证明你的猜想;
满足的数量关系,并证明你的猜想;
② 若三角尺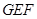 旋转到如图⑶所示的位置时,线段
旋转到如图⑶所示的位置时,线段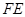 的延长线与
的延长线与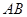 的延长线相交于点
的延长线相交于点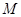 ,线
,线
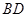 的延长线与
的延长线与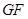 的延长线相交于点
的延长线相交于点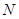 ,此时,①中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
,此时,①中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
【答案】
①结论:BM=FN
证明:∵O是EF的中点,O是BD的中点,且BD=EF
∴EO=F0=OD=OB
∵△ABD和△GEF为等腰直角三角形
∴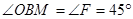
在△FON和△BOM中
 |
∴△FON≌△BOM(ASA)
∴BM=FN
②成立
∵O是EF的中点,O是BD的中点,且BD=EF
∴EO=F0=OD=OB
∵△ABD和△GEF为等腰直角三角形
∴
∴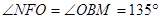
在△FON和△BOM中

∴△FON≌△BOM(ASA)
∴BM=FN
【解析】①找出两三角形全等的条件即可
②仍然利用全等三角形的对应边相等,找出两三角形全等的条件即可

练习册系列答案
相关题目

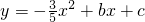 经过A、B、D三点,点G是抛物线的顶点,对称轴GH交x轴为H,动点P从点O沿OB以每秒1个单位的速度向终点B运动,设运动时间为t秒.
经过A、B、D三点,点G是抛物线的顶点,对称轴GH交x轴为H,动点P从点O沿OB以每秒1个单位的速度向终点B运动,设运动时间为t秒.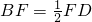 ?(请直接写出答案).
?(请直接写出答案).

 经过A、B、D三点,点G是抛物线的顶点,对称轴GH交x轴为H,动点P从点O沿OB以每秒1个单位的速度向终点B运动,设运动时间为t秒.
经过A、B、D三点,点G是抛物线的顶点,对称轴GH交x轴为H,动点P从点O沿OB以每秒1个单位的速度向终点B运动,设运动时间为t秒.