题目内容
如图,将一张等腰直角三角形纸片沿虚线剪成甲、乙、丙三块,其中甲、丙为直角梯形,乙为等腰直角三角形.根据图中标示的边长数据,比较甲、乙、丙的面积大小,下列判断正确的是( )

A.甲>乙>丙;?? B.乙>丙>甲;?? C.丙>乙>甲;?? D.丙>甲>乙.
【答案】
C.
【解析】
试题分析:首先过点B作BH⊥GF于点H,则S乙=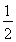 AB•AC,易证得△ABC∽△DBE,△GBH∽△BCA,可求得GF,DB,DE,DF的长,继而求得答案.
AB•AC,易证得△ABC∽△DBE,△GBH∽△BCA,可求得GF,DB,DE,DF的长,继而求得答案.
如图:过点B作BH⊥GF于点H,
则S乙=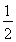 AB•AC,
AB•AC,
∵AC∥DE,
∴△ABC∽△DBE,
∴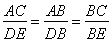 ,
,
∵BC=7,CE=3,
∴DE=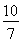 AC,DB=
AC,DB=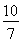 AB,
AB,
∴AD=BD-BA=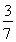 AB,
AB,
∴S丙= (AC+DE)•AD=
(AC+DE)•AD= AB•AC,
AB•AC,
∵A∥GF,BH⊥GF,AC⊥AB,
∴BH∥AC,
∴四边形BDFH是矩形,
∴BH=DF,FH=BD=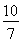 AB,
AB,
∴△GBH∽△BCA,
∴ ,
,
∵GB=2,BC=7,
∴GH= AB,BH=
AB,BH= AC,
AC,
∴DF= AC,GF=GH+FH=
AC,GF=GH+FH= AB,
AB,
∴S甲=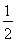 (BD+GF)•DF=
(BD+GF)•DF= AB•AC,
AB•AC,
∴甲<乙,乙<丙.
故选C.
考点: 相似三角形的判定与性质.

练习册系列答案
相关题目
 18、如图,将一张等腰直角三角形纸片沿中位线剪开可以拼成不同形状的四边形,请写出其中一种四边形的名称
18、如图,将一张等腰直角三角形纸片沿中位线剪开可以拼成不同形状的四边形,请写出其中一种四边形的名称 13、如图,将一张等腰直角三角形沿中位线剪成一个三角形与一个梯形后,则这两个图形可能拼成的平面四边形是
13、如图,将一张等腰直角三角形沿中位线剪成一个三角形与一个梯形后,则这两个图形可能拼成的平面四边形是 11、如图,将一张等腰直角三角形纸片沿中位线DE剪开后,可以拼成的四边形是( )
11、如图,将一张等腰直角三角形纸片沿中位线DE剪开后,可以拼成的四边形是( ) 7、如图,将一张等腰直角三角形ABC纸片沿中位线DE剪开后,可以拼成的四边形是( )
7、如图,将一张等腰直角三角形ABC纸片沿中位线DE剪开后,可以拼成的四边形是( ) (2012•孝感模拟)如图,将一张等腰直角△ABC纸片沿中位线DE剪开成两个图形,它们不能拼成的四边形是( )
(2012•孝感模拟)如图,将一张等腰直角△ABC纸片沿中位线DE剪开成两个图形,它们不能拼成的四边形是( )