题目内容
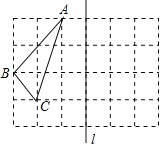
【题目】如图,△ABC中,∠BAC=90°,AB=AC,在△ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
(1)依题意补全图形;
(2)若∠PAC=24°,求∠AEB的度数;
(3)连结CE,若AE=![]() ,CE=1,求BE长.
,CE=1,求BE长.
【答案】(1)图形如图所示:见解析;(2)∠AEB=45°;(3)BE=3.
【解析】
(1)根据要求作出对称点,连线画出图形即可;
(2)根据图形的对称性,得出△ACD和△ADB是等腰三角形,利用∠AEB=∠EAD+∠ADE,求出∠EAD,∠ADE.
(3)在BE上截取BF=ED,连接AF,证明△ABF≌△ADE(SAS),得出BE=DF,利用勾股定理,求出EF即得.
(1)作直线AP,作点C的对称点D,连接AD,BD,图形如图所示:

(2)∵C,D关于PA对称,
∴∠PAC=∠PAD=24°,
∴∠CAD=48°,
∵∠BAC=90°,
∴∠BAD=90°+48°=138°,
∴∠ADB=∠ABD=![]() (180°-138°)=21°,
(180°-138°)=21°,
∴∠AEB=∠EAD+∠ADE=21°+24°=45°.
(3)如图,在BE上截取BF=ED,连接AF,由(1)中作图可知,
AC=AD,CE=DE,
又∵AB=AC,
∴AB=AD,则![]()
在△ABF和△ADE中

∴△ABF≌△ADE(SAS),
∴AF=AE,∠BAF=∠DAE=∠CAE,
∴∠FAE=∠FAC+∠CAE=∠FAC+∠BAC=∠BAC=90°,
∴EF=![]() AE=2,
AE=2,
又BF=ED=CE=1,
∴BE=BF+EF=1+2=3.
故答案为:3.


练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目