Question

【题目】已知和都是等腰直角三角形，.

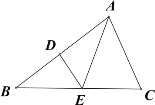
（1）若为上一动点时（如图1），

①求证：.

②试求线段，，间满足的数量关系.

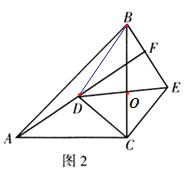
（2）当点在内部时（如图2），延长交于点.

①求证：.

②连结，当为等边三角形时，直接写出与的直角边长之比.

Answer 1

【答案】（1）①证明见解析；②，理由见解析；（2）①证明见解析；②

【解析】

（1）①根据等腰直角三角形的性质和“SAS”证明即可；

②先证明，然后根据勾股定理说明即可；

（2）①由可证，然后利用角的和差即可求出；

②先证明△BCD≌△BEC，从而可得∠DCB=∠ECB=45°，∠DBC=∠EBC=30°，设OC=OE=x，根据勾股定理分别表示出CE和BC的长，然后求比值即可.

（1）①证明：∵和都是等腰直角三角形，，

∴， ，，

∴，

∴，

∴.

②解：∵，

∴，，

∴，

∴，即；

（2）①证明：∵和都是等腰直角三角形，，

∴由（1）易知，

∴，

∴

，

∴，即；

②∵△BDE是等边三角形，

∴BD=BE=DE，

又∵CD=CE，BC=BC，

∴△BCD≌△BEC，

∴∠DCB=∠ECB=45°，∠DBC=∠EBC=30°，

∴BC⊥DE，

∴△COE是等腰直角三角形，

设OC=OE=x，则CE=x，BE=2OE=2x，BO=x，

∴BC=x+x，

∴.