题目内容
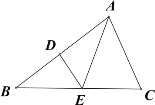
【题目】如图,在△ABC中,AB的垂直平分线分别交AB,BC于点D,E,∠B=30°,∠BAC=80°,且BC+AC=12cm,①求∠CAE的度数;②求△AEC的周长。
【答案】①50°;②12cm.
【解析】
①依据AB的垂直平分线分别交AB,BC于点D,E,即可得出BE=AE,进而得到∠BAE=∠B=30°,再根据∠CAE=∠BAC-∠BAE进行计算即可;
②根据BE=AE,利用BC+AC=12cm,即可求出△AEC的周长.
解:①∵AB的垂直平分线分别交AB,BC于点D,E,
∴BE=AE,
∴∠BAE=∠B=30°,
又∵∠BAC=80°,
∴∠CAE=∠BAC-∠BAE=80°-30°=50°,
②由①得BE=AE,
∴△AEC的周长= AE+EC+AC =BE+EC+AC =BC+AC=12cm

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
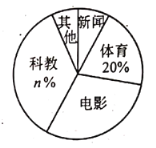
【题目】学校为了解全校![]() 名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
频道 | 新闻 | 体育 | 电影 | 科教 | 其他 |
人数 |
|
|
|
|
|
![]() 求调查的学生人数及统计图表中
求调查的学生人数及统计图表中![]() 的值;
的值;
![]() 求选择其他频道在统计图中对应扇形的圆心角的度数;
求选择其他频道在统计图中对应扇形的圆心角的度数;
![]() 求全校最爱选择电影频道的学生人数.
求全校最爱选择电影频道的学生人数.