题目内容
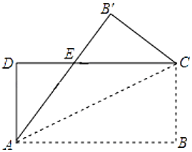
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 上的动点.
上的动点.

(1)能否在线段![]() 上作出点E,在线段
上作出点E,在线段![]() 上作出点
上作出点![]() ,使
,使![]() 的周长最小?______(用“能”或“不能”填空);
的周长最小?______(用“能”或“不能”填空);
(2)如果能,请你在图中作出满足条件的点![]() 、
、![]() (不要求写出作法),并直接写出
(不要求写出作法),并直接写出![]() 的度数;如果不能,请说明理由.
的度数;如果不能,请说明理由.
【答案】(1)能;(2)作出满足条件的点![]() 、
、![]() (图见解析),
(图见解析),![]()
【解析】
(1)根据对称性能在线段AD上作出点E,在线段DC上作出点F,使△BEF的周长最小;
(2)根据对称性得等腰三角形,再根据三角形内角和即可求出∠EBF的度数.
解:(1)能在线段AD上作出点E,在线段DC上作出点F,使△BEF的周长最小.
故答案为:能.
(2)如图所示: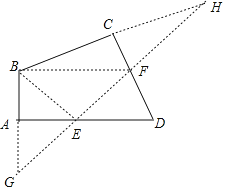
点E、F即为所求作的点.
作点B关于AD和DC的对称点G和H,
连接GH,交AD和DC于点E和F,
连接BE、BF,此时△BEF的周长最小.
由对称性可知:
BF=HF,BE=GE,
∴∠FBH=∠H,∠EBG=∠G,
∵四边形ABCD中,∠D=70°,∠A=∠C=90°,
∴∠ABC=110°,
∴∠H+∠G=70°,
∴∠FBH+∠EBG=70°,
∴∠EBF=110°-70°=40°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
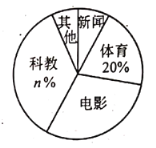
【题目】学校为了解全校![]() 名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
频道 | 新闻 | 体育 | 电影 | 科教 | 其他 |
人数 |
|
|
|
|
|
![]() 求调查的学生人数及统计图表中
求调查的学生人数及统计图表中![]() 的值;
的值;
![]() 求选择其他频道在统计图中对应扇形的圆心角的度数;
求选择其他频道在统计图中对应扇形的圆心角的度数;
![]() 求全校最爱选择电影频道的学生人数.
求全校最爱选择电影频道的学生人数.