题目内容
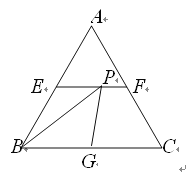
【题目】将一块直角三角板DEF放置在锐角△ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C.

(1)如图①,若∠A=40°时,点D在△ABC内,则∠ABC+∠ACB= 度,∠DBC+∠DCB= 度,∠ABD+∠ACD= 度;
(2)如图②,改变直角三角板DEF的位置,使点D在△ABC内,请探究∠ABD+∠ACD与∠A之间存在怎样的数量关系,并验证你的结论.
(3)如图③,改变直角三角板DEF的位置,使点D在△ABC外,且在AB边的左侧,直接写出∠ABD、∠ACD、∠A三者之间存在的数量关系.
【答案】(1)140,90,50;(2)∠ABD+∠ACD=90°﹣∠A,证明见解析;(3)∠ACD﹣∠ABD=90°﹣∠A.
【解析】
(1)根据三角形内角和定理可得∠ABC+∠ACB=180°﹣∠A=140°,∠DBC+∠DCB=180°﹣∠DBC=90°,进而可求出∠ABD+∠ACD的度数;
(2)根据三角形内角和定义有90°+(∠ABD+∠ACD)+∠A=180°,则∠ABD+∠ACD=90°﹣∠A.
(3)设线段DC和线段AB交于点O,根据三角形外角的性质可得:∠ACD﹣∠ABD=90°﹣∠A.
(1)在△ABC中,∵∠A=40°,∴∠ABC+∠ACB=180°﹣40°=140°,
在△DBC中,∵∠BDC=90°,∴∠DBC+∠DCB=180°﹣90°=90°,∴∠ABD+∠ACD=140°﹣90°=50°.
故答案为:140,90,50.
(2)∠ABD+∠ACD与∠A之间的数量关系为:∠ABD+∠ACD=90°﹣∠A.证明如下:
在△ABC中,∠ABC+∠ACB=180°﹣∠A.
在△DBC中,∠DBC+∠DCB=90°,∴∠ABC+∠ACB﹣(∠DBC+∠DCB)=180°﹣∠A﹣90°,∴∠ABD+∠ACD=90°﹣∠A.
(3)∠ACD﹣∠ABD=90°﹣∠A.证明如下:
设线段DC和线段AB交于点O.
∵∠BOC=∠D+∠DBO=∠A+∠ACO,∴90°+∠ABD=∠A+∠ACD,∴∠ACD﹣∠ABD=90°﹣∠A.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案