题目内容
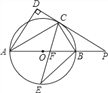
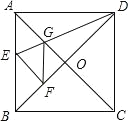
【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折叠DE分别交AB、AC于E、G,连接GF,下列结论:①∠FGD=112.5°②BE=2OG③S△AGD=S△OGD④四边形AEFG是菱形( )
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
①由四边形ABCD是正方形和折叠性得出∠DAG=∠DFG=45°,∠ADG=∠FDG=45°÷2=22.5°,再由三角形的内角和求出∠FGD=112.5°.故①正确,
②④由四边形ABCD是正方形和折叠,判断出四边形AEFG是平行四边形,再由AE=EF,得出四边形AEFG是菱形.利用45°的直角三角形得出GF=![]() OG,BE=
OG,BE=![]() EF=
EF=![]() GF,得出BE=2OG,故②④正确.
GF,得出BE=2OG,故②④正确.
③由四边形ABCD是正方形和折叠性,得到△ADG≌△FDG,所以S△AGD=S△FDG≠S△OGD故③错误.
①由四边形ABCD是正方形和折叠性知,
∠DAG=∠DFG=45°,∠ADG=∠FDG=45°÷2=22.5°,
∴∠FGD=180°﹣∠DFG﹣∠FDG=180°﹣45°﹣22.5°=112.5°,
故①正确,
②由四边形ABCD是正方形和折叠性得出,
∠DAG=∠DFG=45°,∠EAD=∠EFD=90°,AE=EF,
∵∠ABF=45°,
∴∠ABF=∠DFG,
∴AB∥GF,
又∵∠BAC=∠BEF=45°,
∴EF∥AC,
∴四边形AEFG是平行四边形,
∴四边形AEFG是菱形.
∵在Rt△GFO中,GF=![]() OG,
OG,
在Rt△BFE中,BE=![]() EF=
EF=![]() GF,
GF,
∴BE=2OG,
故②④正确.
③由四边形ABCD是正方形和折叠性知,
AD=FD,AG=FG,DG=DG,
在△ADG和△FDG中,
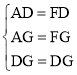 ,
,
∴△ADG≌△FDG(SSS),
∴S△AGD=S△FDG≠S△OGD
故③错误.
正确的有①②④,
故选C.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案