题目内容
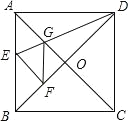
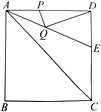
【题目】如图，正方形
的边长是
，
的平分线交
于点
，若点
分别是
和
上的动点，则
的最小值是_______.
【答案】
【解析】
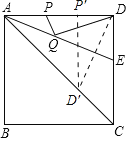
过D作AE的垂线交AE于F，交AC于D′，再过D′作D′P′⊥AD，由角平分线的性质可得出D′是D关于AE的对称点，进而可知D′P′即为DQ+PQ的最小值.
解：解：作D关于AE的对称点D′，再过D′作D′P′⊥AD于P′，
∵DD′⊥AE，
∴∠AFD=∠AFD′，
∵AF=AF，∠DAE=∠CAE，
∴△DAF≌△D′AF，
∴D′是D关于AE的对称点，AD′=AD=5，
∴D′P′即为DQ+PQ的最小值，
∵四边形ABCD是正方形，
∴∠DAD′=45°，
∴AP′=P′D′，
∴在Rt△AP′D′中，
P′D′2+AP′2=AD′2，AD′2=25，
∵AP′=P′D'，
2P′D′2=AD′2，即2P′D′2=25，
，即DQ+PQ的最小值为.
练习册系列答案
相关题目
【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛，在最近的五次选拔测试中，他俩的成绩分别如下表：
次数 | 1 | 2 | 3 | 4 | 5 |
小王 | 60 | 75 | 100 | 90 | 75 |
小李 | 70 | 90 | 100 | 80 | 80 |
根据上表解答下列问题：
（1）完成下表：
姓名 | 平均成绩（分） | 中位数（分） | 众数（分） | 方差 |
小王 | 80 | 75 | 75 | 190 |
小李 |
（2）在这五次测试中，成绩比较稳定的同学是谁？若将80分以上（含80分）的成绩视为优秀，则小王、小李在这五次测试中的优秀率各是多少？
（3）历届比赛表明，成绩达到80分以上（含80分）就很可能获奖，成绩达到90分以上（含90分）就很可能获得一等奖，那么你认为选谁参加比赛比较合适？说明你的理由．
