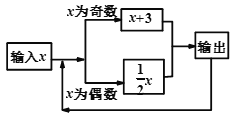
题目内容
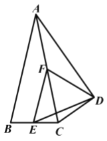
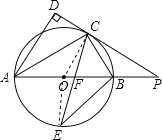
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE.
(1)求证:AC平分∠DAB;
(2)探究线段PC,PF之间的大小关系,并加以证明;
(3)若tan∠PCB=![]() ,BE=
,BE=![]() ,求PF的长.
,求PF的长.
【答案】(1)见解析;(2)PC=PF.证明见解析;(3)![]() .
.
【解析】试题分析:(1)、连接OC,根据切线的性质得出∠OCP=∠D=90°即 OC∥AD,然后根据OA=OC得出∠CAD=∠OCA=∠OAC,从而得出角平分线;(2)、根据∠PCB+∠ACD=∠CAD+∠ACD=90°,从而得出∠CAB=∠CAD=∠PCB,结合∠ACE=∠BCE,∠PFC=∠CAB+∠ACE,∠PCF=∠PCB+∠BCE得出∠PFC=∠PCF,从而得出答案;(3)、连接AE,根据题意得出△PCB和△PAC相似,然后设PB=3x,则PC=4x,根据Rt△POC的勾股定理得出x的值,从而得出答案.
试题解析:(1)连接OC. ∵OA=OC,∴∠OAC=∠OCA.
∵PC是⊙O的切线,AD⊥CD, ∴∠OCP=∠D=90°, ∴ OC∥AD.
∴ ∠CAD=∠OCA=∠OAC.即AC平分∠DAB.
(2)PC=PF.
证明:∵AB是直径, ∴∠ACB=90°,∴∠PCB+∠ACD=90° 又∵∠CAD+∠ACD=90°,
∴∠CAB=∠CAD=∠PCB.
又∵∠ACE=∠BCE,∠PFC=∠CAB+∠ACE,∠PCF=∠PCB+∠BCE. ∴∠PFC=∠PCF.
∴PC=PF.
(3)连接AE. ∵∠ACE=∠BCE,∴![]() =
=![]() , ∴AE=BE.
, ∴AE=BE.
又∵AB是直径, ∴∠AEB=90°.AB=![]() , ∴OB=OC=5.
, ∴OB=OC=5.
∵∠PCB=∠PAC,∠P=∠P, ∴△PCB∽△PAC. ∴![]() .
.
∵tan∠PCB=tan∠CAB=![]() , ∴
, ∴![]() =
=![]() .
.
设PB=3x,则PC=4x,在Rt△POC中,(3x+5)2=(4x)2+52,
解得x1=0,![]() . ∵x>0,∴
. ∵x>0,∴![]() , ∴PF=PC=
, ∴PF=PC=![]() .
.

【题目】为了解某校七年级男生的身高(单位:![]() )情况,随机抽取了七年级部分学生进行了抽样调查.统计数据如下表:
)情况,随机抽取了七年级部分学生进行了抽样调查.统计数据如下表:
组别 |
|
|
|
|
|
身高 |
|
|
|
|
|
人数 |
|
|
|
|
|
(1)样本容量是多少?组距是多少?组数是多少?
(2)画出适当的统计图表示上面的信息;
(3)若全校七年级学生有![]() 人,请估计身高不低于
人,请估计身高不低于![]() 的学生人数.
的学生人数.