题目内容
【题目】如图,抛物线C1:y1=tx2﹣1(t>0)和抛物线C2:y2=﹣4(x﹣h)2+1(h≥1).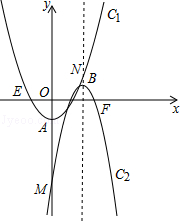
(1)两抛物线的顶点A、B的坐标分别为和;
(2)设抛物线C2的对称轴与抛物线C1交于点N,则t为何值时,A、B、M、N为顶点的四边形是平行四边形.
(3)设抛物线C1与x轴的左交点为点E,抛物线C2与x轴的右边交点为点F,试问,在第(2)问的前提下,四边形AEBF能否为矩形?若能,求出h值;若不能,说明理由.
【答案】
(1)(0,1);(h,1)
(2)
解:∵AM∥BN,
∴当AM=BN时,A、B、M、N为顶点的四边形是平行四边形,
∵当x=h时,y1=1,y2=tx2﹣1=th2﹣1,
∴PN=|1﹣(th2﹣1)\=|2﹣th2|.
①当点B在点A的下方时,4h2﹣2=th2﹣2,∵h2≠0,∴t=4;
②当点B在点A的上方时,4h2﹣2=2﹣th2,整理,得t+4= ![]() ,
,
∵t>0时,t+4>4;当h≥1时, ![]() ≤4,
≤4,
∴这样的t值不存在,
答:当点B在点A的下方时,t=4,当点B在点A的上方时不存在
(3)
解:由(2)可知,二次项系数互为相反数,
∴两抛物线的形状相同,故它们成中心对称,
∵点A和点B的纵坐标的绝对值相同,
∴两抛物线得对称中心落在x轴上.
∵四边形AEBF是平行四边形,
∴当∠EAF=90°时,四边形AFBE是矩形,
∵抛物线C1与x轴左交点坐标是(﹣ ![]() ,0),
,0),
∴OE= ![]() .
.
∵抛物线C2与x轴右交点坐标是(h+ ![]() ,0)且h≥1,
,0)且h≥1,
∴OF=h+ ![]() .
.
∵∠FAO+∠EAO=90°,∠EAO+AEO=90°,
∴∠FAO=∠AEO,
又∵∠FOA=∠EOA=90°,
∴△AEO∽△FAO, ![]() =
= ![]()
∴OA2=OEOF,即 ![]() (h+
(h+ ![]() )=1,解得h=
)=1,解得h= ![]() >1,
>1,
∴四边形AEBF能为矩形,且h的值为 ![]()
【解析】解:(1)抛物线C1:y1=tx2﹣1的顶点坐标是(0,﹣1),
抛物线C2:y2=﹣4(x﹣h)2+1的顶点坐标是(h,1),
所以答案是:(0,﹣1),(h,1);