题目内容
【题目】阅读理解:在以后你的学习中,我们会学习一个定理:直角三角形斜边上的中线等于斜边的一半,即:如图1,

在![]() 中,
中,![]() °,若点
°,若点![]() 是斜边
是斜边![]() 的中点,则
的中点,则![]() .
.
灵活应用:如图2,![]() 中,
中,![]() °,
°,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,

将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,连接
,连接![]() ,
,![]() .
.
(1)求![]() 的长:
的长:
(2)判断![]() 的形状:
的形状:
(3)请直接写出![]() 的长.
的长.
【答案】(1)![]() ;(2)直角三角形;(3)
;(2)直角三角形;(3)![]()
【解析】(1)利用直角三角形斜边上的中线等于斜边的一半,即可得出答案;
(2)利用直角三角形斜边上的中线等于斜边的一半及线段中点定义,得到CD=DE=DB,再利用等腰三角形的性质及三角形内角和定理即可得出结论;
(3)连接BE交AD于O,作AH⊥BC于H.首先证明AD垂直平分线段BE,求出BE,在Rt△BCE中,利用勾股定理即可解决问题.
解:(1)![]() 点
点![]() 是
是![]() 的终点,
的终点,![]() 为
为![]() 的斜边,
的斜边,
![]() .
.
(2)![]() 是
是![]() 的中点,
的中点,
![]()
![]() 将
将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() °,
°,
![]() ,
,
![]() °,
°,
![]() 是直角三角形.
是直角三角形.
(3)如图连接BE交AD于O,作AH⊥BC于H.
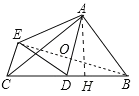
在Rt△ABC中,∵AC=4,AB=3,
∴BC=5,
∵CD=DB,
∴AD=DC=DB=![]() ,
,
∵![]() BCAH=
BCAH=![]() ABAC,
ABAC,
∴AH=![]() ,
,
∵AE=AB,DE=DB=DC,
∴AD垂直平分线段BE,
∵![]() ADBO=
ADBO=![]() BDAH,
BDAH,
∴OB=![]() ,
,
∴BE=2OB=![]() ,
,
在Rt△BCE中,EC![]() .
.

练习册系列答案
相关题目
