题目内容
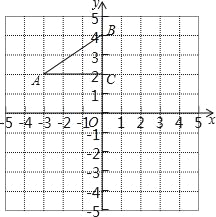
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请在图中标明旋转中心P的位置并写出其坐标.
【答案】(1)见解析;(2) (![]() ,﹣1)
,﹣1)
【解析】试题分析:(1)按题意画出图形即可;(2)A1与A2对应,B1与B2对应,连接A1 A2、B1 B2,交点即为点P.
试题解析:
解:(1)如图,△A1B1C和△A2B2C2为所作;

(2)如图,点P为所作,
由图像可得:A1(3,2),A2(0,-4),B1(0,0),B2(3,-2),
设直线A1A2解析式为y=kx+b,
则![]() ,
,
解得![]() ,
,
∴直线A1A2的解析式为y=2x-4,
设直线B1B2解析式为y=ax,
3a=-2,
解得a=-![]() ,
,
∴直线A1A2的解析式为y=-![]() x,
x,
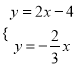 ,
,
解得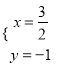 .
.
∴P点坐标为(![]() ,-1).
,-1).

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目