Question

【题目】（问题情境）

张老师给爱好学习的小军和小俊提出这样的一个问题：如图1，在△ABC中，AB＝AC，点P为边BC上任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D，E，过点C作CF⊥AB，垂足为F，求证：PD+PE＝CF．

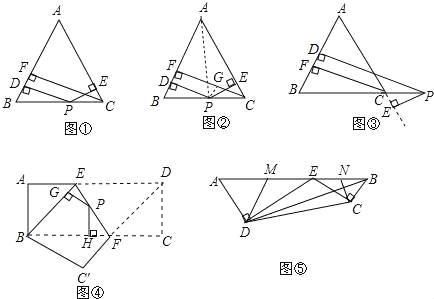
小军的证明思路是：如图2，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE＝CF．

小俊的证明思路是：如图2，过点P作PG⊥CF，垂足为G，可以证得：PD＝GF，PE＝CG，则PD+PE＝CF．

[变式探究]

如图3，当点P在BC延长线上时，其余条件不变，求证：PD﹣PE＝CF；

请运用上述解答中所积累的经验和方法完成下列两题：

[结论运用]

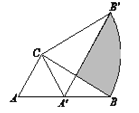
如图4，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点C′处，点P为折痕EF上的任一点，过点P作PG⊥BE、PH⊥BC，垂足分别为G、H，若AD＝8，CF＝3，求PG+PH的值；

[迁移拓展]

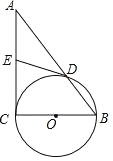
图5是一个航模的截面示意图．在四边形ABCD中，E为AB边上的一点，ED⊥AD，EC⊥CB，垂足分别为D、C，且ADCE＝DEBC，AB＝2dm，AD＝3dm，BD＝dm．M、N分别为AE、BE的中点，连接DM、CN，求△DEM与△CEN的周长之和．

Answer 1

【答案】小军的证明：见解析；小俊的证明：见解析；[变式探究]见解析；[结论运用]PG+PH的值为4；[迁移拓展]（6+2）dm

【解析】

小军的证明：连接AP，利用面积法即可证得；

小俊的证明：过点P作PG⊥CF，先证明四边形PDFG为矩形，再证明△PGC≌△CEP，即可得到答案；

[变式探究]小军的证明思路：连接AP，根据S△ABC＝S△ABP﹣S△ACP，即可得到答案；

小俊的证明思路：过点C，作CG⊥DP，先证明四边形CFDG是矩形，再证明△CGP≌△CEP即可得到答案；

[结论运用] 过点E作EQ⊥BC，先根据矩形的性质求出BF，根据翻折及勾股定理求出DC，证得四边形EQCD是矩形，得出BE＝BF即可得到答案；

[迁移拓展]延长AD，BC交于点F，作BH⊥AF，证明△ADE∽△BCE得到FA=FB，设DH＝x，利用勾股定理求出x得到BH＝6，再根据∠ADE＝∠BCE＝90°，且M，N分别为AE，BE的中点即可得到答案.

小军的证明：

连接AP，如图②

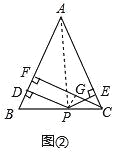
∵PD⊥AB，PE⊥AC，CF⊥AB，

∴S△ABC＝S△ABP+S△ACP，

∴AB×CF＝AB×PD+AC×PE，

∵AB＝AC，

∴CF＝PD+PE．

小俊的证明：

过点P作PG⊥CF，如图2，

∵PD⊥AB，CF⊥AB，PG⊥FC，

∴∠CFD＝∠FDG＝∠FGP＝90°，

∴四边形PDFG为矩形，

∴DP＝FG，∠DPG＝90°，

∴∠CGP＝90°，

∵PE⊥AC，

∴∠CEP＝90°，

∴∠PGC＝∠CEP，

∵∠BDP＝∠DPG＝90°，

∴PG∥AB，

∴∠GPC＝∠B，

∵AB＝AC，

∴∠B＝∠ACB，

∴∠GPC＝∠ECP，

在△PGC和△CEP中

，

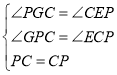∴△PGC≌△CEP，

∴CG＝PE，

∴CF＝CG+FG＝PE+PD；

[变式探究]

小军的证明思路：连接AP，如图③，

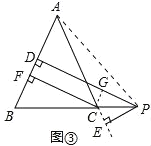
∵PD⊥AB，PE⊥AC，CF⊥AB，

∴S△ABC＝S△ABP﹣S△ACP，

∴AB×CF＝AB×PD﹣AC×PE，

∵AB＝AC，

∴CF＝PD﹣PE；

小俊的证明思路：

过点C，作CG⊥DP，如图③，

∵PD⊥AB，CF⊥AB，CG⊥DP，

∴∠CFD＝∠FDG＝∠DGC＝90°，

∴CF＝GD，∠DGC＝90°，四边形CFDG是矩形，

∵PE⊥AC，

∴∠CEP＝90°，

∴∠CGP＝∠CEP，

∵CG⊥DP，AB⊥DP，

∴∠CGP＝∠BDP＝90°，

∴CG∥AB，

∴∠GCP＝∠B，

∵AB＝AC，

∴∠B＝∠ACB，

∵∠ACB＝∠PCE，

∴∠GCP＝∠ECP，

在△CGP和△CEP中，

，

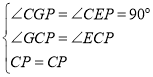∴△CGP≌△CEP，

∴PG＝PE，

∴CF＝DG＝DP﹣PG＝DP﹣PE．

[结论运用]

如图④

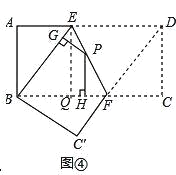
过点E作EQ⊥BC，

∵四边形ABCD是矩形，

∴AD＝BC，∠C＝∠ADC＝90°，

∵AD＝8，CF＝3，

∴BF＝BC﹣CF＝AD﹣CF＝5，

由折叠得DF＝BF，∠BEF＝∠DEF，

∴DF＝5，

∵∠C＝90°，

∴DC＝＝4，

∵EQ⊥BC，∠C＝∠ADC＝90°，

∴∠EQC＝90°＝∠C＝∠ADC，

∴四边形EQCD是矩形，

∴EQ＝DC＝4，

∵AD∥BC，

∴∠DEF＝∠EFB，

∵∠BEF＝∠DEF，

∴∠BEF＝∠EFB，

∴BE＝BF，

由问题情景中的结论可得：PG+PH＝EQ，

∴PG+PH＝4．

∴PG+PH的值为4．

[迁移拓展]

延长AD，BC交于点F，作BH⊥AF，如图⑤，

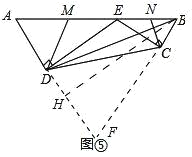
∵AD×CE＝DE×BC，

∴，

∵ED⊥AD，EC⊥CB，

∴∠ADE＝∠BCE＝90°，

∴△ADE∽△BCE，

∴∠A＝∠CBE，

∴FA＝FB，

由问题情景中的结论可得：ED+EC＝BH，

设DH＝x，

∴AH＝AD+DH＝3+x，

∵BH⊥AF，

∴∠BHA＝90°，

∴BH2＝BD2﹣DH2＝AB2﹣AH2，

∵AB＝2，AD＝3，BD＝，

∴（）2﹣x2＝（2）2﹣（3+x）2，

∴x＝1，

∴BH2＝BD2﹣DH2＝37﹣1＝36，

∴BH＝6，

∴ED+EC＝6，

∵∠ADE＝∠BCE＝90°，且M，N分别为AE，BE的中点，

∴DM＝EM＝AE，CN＝EN＝BE，

∴△DEM与△CEN的周长之和

＝DE+DM+EM+CN+EN+EC

＝DE+AE+BE+EC

＝DE+AB+EC

＝DE+EC+AB

＝6+2，

∴△DEM与△CEN的周长之和（6+2）dm．