题目内容
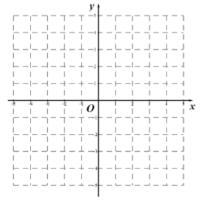
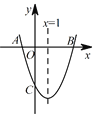
【题目】已知，如图，有一块含有30°的直角三角形
的直角边
的长恰与另一块等腰直角三角形
的斜边
的长相等．把该套三角板放置在平面直角坐标系中，且
（1）若某开口向下的抛物线的顶点恰好为点
，请写出一个满足条件的抛物线的解析式．
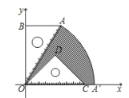
（2）若把含30°的直角三角形绕点
按顺时针方向旋转后，斜边
恰好与轴重叠，点落在点
，试求图中阴影部分的面积（结果保留
）
【答案】（1）
；（2）
【解析】
（1）在Rt△OBA中，由∠AOB=30°，AB=3利用特殊角的正切值即可求出OB的长度，从而得出点A的坐标，利用顶点式即可求出函数解析式；
（2）在Rt△OBA中，利用勾股定理即可求出OA的长度，在等腰直角三角形ODC中，根据OC的长度可求出OD的长，结合图形即可得出阴影部分的面积为扇形AOA′的面积减去三角形ODC的面积，结合扇形与三角形的面积公式即可得出结论．
解：（1）在
中，
，
∴
∴
∴
．
∴抛物线的解析式是
（2）由（1）可知
，由题意得
∴
在
中，
∴
∴
练习册系列答案
小学期末标准试卷系列答案
相关题目
