Question

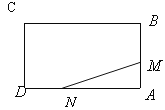
【题目】如图，已知矩形的边长．某一时刻，动点从点出发沿方向以的速度向点匀速运动；同时，动点从点出发沿方向以的速度向点匀速运动，问：

（1）经过多少时间，的面积等于矩形面积的？

（2）是否存在时间t,使的面积达到3.5cm2，若存在，求出时间t，若不存在，说明理由．

Answer 1

【答案】（1）经过1s或2t，的面积等于矩形面积的，

(2)不存在，理由见解析

【解析】

（1）易得AM，AN的长，利用△AMN的面积等于矩形ABCD面积的列出等式求解即可．

（2）假设存在时间t，使的面积达到3.5，则，用△AMN的面积等于3.5列出方程，根据根的判别式即可判断．

解：（1）设经过ts，的面积等于矩形面积的,

则DN=2t,AM=t，AN=AD-DN=6-2t

∵

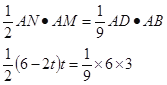
∴t1="1" t2=2

∴经过1s或2t，的面积等于矩形面积的，

(2)不存在，

理由：假设存在时间t，使的面积达到3.5，则，

,

∵

∴方程没有实数根,

∴假设不成立，

∴的面积不能达到3.5．