Question

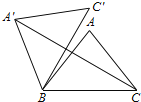
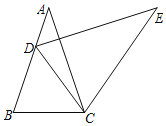
【题目】如图，△ABC中，AB＝AC＝2，tanB＝3，点D为边AB上一动点，在直线DC上方作∠EDC＝∠ECD＝∠B，得到△EDC，则CE最小值为_____．

Answer 1

【答案】6.

【解析】

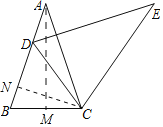
作AM⊥BC于M，CN⊥AB于N．在Rt△ABM中，根据三角函数关系可求得BM，AM的值，在Rt△CNB中根据三角函数关系可求得NC的值.易证明△EDC∽△ABC，根据相似的性质可得，可得DC最小时，EC最小，当DC与NC重合时DC最小，由此可求得CE.

作AM⊥BC于M，CN⊥AB于N．

∵AB＝AC，AM⊥BC，

∴BM＝MC，∠B＝∠ACB，

∴tanB＝＝3，设AM＝3k，BM＝k，

在Rt△ABM中，40＝9k2+k2，

∴k2＝4，

∵k＞0，

∴k＝2，

∴BM＝CM＝2，BC＝4，

∵CN⊥AB，

∴∠CNB＝90°，

∴tanB＝＝3，设BN＝m，CN＝3m，

则有，10m2＝16，

∵m＞0，

∴m＝，

∴CN＝，

∵∠EDC＝∠ECD＝∠B＝∠ACB，

∴△EDC∽△ABC，

∴＝，

∴＝＝，

∴DC最小时，EC的值最小，

∵当CD与CN重合时CD的值最小，此时CD＝，

∴EC的最小值＝×2÷4＝6，

故答案为6．