题目内容
矩形ABCD中,AB=8,BC=3,点P在边AB上,且BP=3AP,如果圆P是以点P为圆心,PD为半径的圆,那么下列判断正确的是( )
A.点B、C均在圆P外 B.点B在圆P外、点C在圆P内
C.点B在圆P内、点C在圆P外 D.点B、C均在圆P内
A.点B、C均在圆P外 B.点B在圆P外、点C在圆P内
C.点B在圆P内、点C在圆P外 D.点B、C均在圆P内
C
试题分析:根据BP=3AP和AB的长度求得AP的长,然后利用勾股定理求得圆P的半径PD的长,根据点B、C到P点的距离判断点P与圆的位置关系即可.
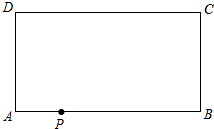
∵AB=8,点P在边AB上,且BP=3AP,
∴AP=2,
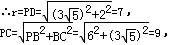
∵PB=6<7,PC=9>7
∴点B在圆P内、点C在圆P外
故选C.
点评:根据点与圆心之间的距离和圆的半径的大小关系作出判断是解题的关键.

练习册系列答案
相关题目
 与x轴交于点A,与y轴交于点B,点C(0,2)、点M(m,0),如果以MC为半径的⊙M与直线AB相切,则经过点A、C、M的抛物线的解析式为________.
与x轴交于点A,与y轴交于点B,点C(0,2)、点M(m,0),如果以MC为半径的⊙M与直线AB相切,则经过点A、C、M的抛物线的解析式为________.
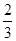 ,∠A=30º.
,∠A=30º.
 的长;
的长;