题目内容
【题目】点D、E分别是△ABC两边AB、BC所在直线上的点,∠BDE+∠ACB=180°,DE=AC,AD=2BD.


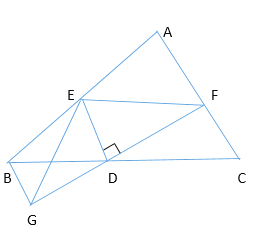
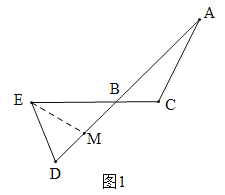
(1) 如图1,当点D、E分别在AB、CB的延长线上时,求证:BE=BD
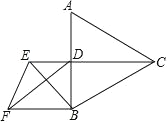
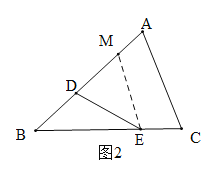
(2) 如图2,当点D、E分别在AB、BC边上时,BE与BD存在怎样的数量关系?请写出你的结论,并证明
【答案】(1)证明见解析;(2)BE=3BD
【解析】
(1)在BD上找一点M,连接EM,使EM=ED,如图1.证明![]()
可得EB=AB,利用AD=2BD,AB=AD-BD即可得结论;
(2)在AB上找一点M,连接EM,使EM=ED,如图2.证明![]() 可得
可得![]() 由AD=2BD,可得AB=AD+BD=3BD代入,即可得结论.
由AD=2BD,可得AB=AD+BD=3BD代入,即可得结论.
(1)在BD上找一点M,连接EM,使EM=ED,如图1.
则∠BDE=∠EMD.
∵∠BDE+∠ACB=180°,
∴∠EMB=∠ACB.
∵DE=AC,
∴EM=AC
在△EMB和△ACB中,

![]()
∴EB=AB
∵AD=2BD,
∴AB=AD-BD=BD.
∴BE=BD;
(2) BE=3BD,理由如下:在AB上找一点M,连接EM,使EM=ED,如图2.
则∠MDE=∠EMD.
∵DE=AC,
∴EM=AC.
∵∠BDE+∠ACB=180, ∠EDM+∠BDE=180,
∴∠EMD=∠ACB
∵∠EBM=∠ABC,
![]()
![]()
∵AD=2BD,
∴AB=AD+BD=3BD
![]() .
.
∴BE=3BD

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目