Question

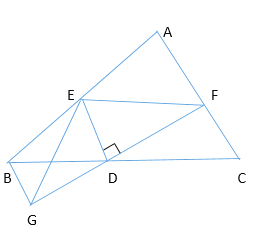
【题目】如图，在△ABC中，D是BC中点，过点D的直线GF交AC于F，交AC的平行线BG于G，DE⊥DF，交AB于E,连接BG，请你判断BE+CF与EF的大小关系，请说明理由.

Answer 1

【答案】BE+CF＞EF，理由见解析

【解析】

求出∠C=∠GBD，BD=DC，根据ASA证出△CFD≌△BGD，根据全等得出GD=DF，BG=CF，根据线段垂直平分线性质得出EG=EF，再根据三角形三边关系定理求出即可．

∵BG∥AC，

∴∠C=∠GBD，

∵D是BC的中点，

∴BD=DC，

在△CFD和△BGD中

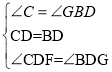
∴△CFD≌△BGD（ASA），

∴DG=DF，

∵DE⊥GF，

∴EG=EF；

∴CF=BG，

在△BGE中，BE+ BG＞EG，

∴BE+CF＞EF．