Question

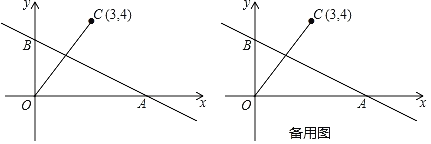
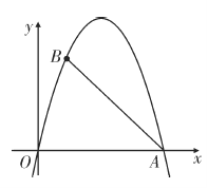
【题目】如图，抛物线与轴交于点，，与轴交于点，直线为.

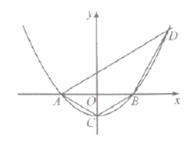
（1）求抛物线的解析式.

（2）过点作直线与抛物线在第一象限的交点为.当时，确定直线与的位置关系.

（3）在第二象限抛物线上求一点，使.

Answer 1

【答案】（1）（2）（3）（-6,4）

【解析】

（1）根据直线可以求出B,C，设出抛物线的解析式，代入即可得出答案；

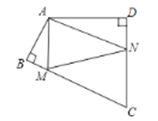
（2）作轴于，可得到，根据可得，由可得，根据题意得到，代入设出的解析式即可求解；

（3）根据（2）可得，，，可得出，，能够推出是等腰三角形，得到，当时，，得到直线为，根据可求得结果．

解：（1）由直线知，，．

可设抛物线解析式为．

将代入，得．

．

抛物线的解析式为

（2）作轴于．由（1），得．

与有公共边，，

．

由，得．正数．

．

由题意，.

设直线为．

解得，．直线为．

．

（3）由（2），，，．

．，．

在中，由勾股定理，得．

．

是等腰三角形．

．

当时，．

直线为．

由，得．

，．

．

点的坐标为．