题目内容
【题目】如图,二次函数y2=ax2+bx+3的图象与x轴相交于点A(3,0)、B(1,0),交y轴于点C,C、D是二次函数图象上的一对对称点,一次函数y1=mx+n的图象经过B. D两点.
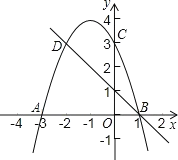
(1)求a、b的值及点D的坐标;
(2)根据图象写出y2>y1时,x的取值范围.
【答案】(1)a=-1,b=-2, D(-2,3);(2)2<x<0
【解析】
(1)由于已知抛物线与x轴的交点坐标,则设交点式y=a(x+3)(x-1)=![]() ,则-3a=3,解得a=-1,所以b=-2,抛物线的对称轴为直线x=-1,再求出C点坐标为(0,3),然后根据对称的性质确定D点坐标为(-2,3);
,则-3a=3,解得a=-1,所以b=-2,抛物线的对称轴为直线x=-1,再求出C点坐标为(0,3),然后根据对称的性质确定D点坐标为(-2,3);
(2)观察函数图象得到当-2<x<0时,抛物线都在直线y=mx+n的上方,即y2>y1.
(1)设抛物线解析式为y=a(x+3)(x1)= ![]() ,
,
则3a=3,解得a=1,
所以抛物线解析式为y=![]() ;
;
所以b=2,
抛物线的对称轴为直线x=1,
当x=0时, ![]() ,则C点坐标为(0,3),
,则C点坐标为(0,3),
由于C. D是二次函数图象上的一对对称点,
∴D点坐标为(2,3);
(2)观察函数图象得到当-2<x<0时,抛物线都在直线y=mx+n的上方,即y2>y1.当2<x<0时, ![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目