题目内容
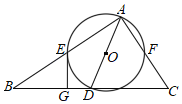
【题目】在△ABC中,以AB边上的中线CD为直径作圆,如果与边AB有交点E(不与点D重合),那么称![]() 为△ABC的C﹣中线弧.例如,如图中
为△ABC的C﹣中线弧.例如,如图中![]() 是△ABC的C﹣中线弧.在平面直角坐标系xOy中,已知△ABC存在C﹣中线弧,其中点A与坐标原点O重合,点B的坐标为(2t,0)(t>0).
是△ABC的C﹣中线弧.在平面直角坐标系xOy中,已知△ABC存在C﹣中线弧,其中点A与坐标原点O重合,点B的坐标为(2t,0)(t>0).
(1)当t=2时,
①在点C1(﹣3,2),C2(0,2![]() ),C3(2,4),C4(4,2)中,满足条件的点C是 ;
),C3(2,4),C4(4,2)中,满足条件的点C是 ;
②若在直线y=kx(k>0)上存在点P是△ABC的C﹣中线弧![]() 所在圆的圆心,其中CD=4,求k的取值范围;
所在圆的圆心,其中CD=4,求k的取值范围;
(2)若△ABC的C﹣中线弧![]() 所在圆的圆心为定点P(2,2),直接写出t的取值范围.
所在圆的圆心为定点P(2,2),直接写出t的取值范围.
【答案】(1)①C2,C4;②![]() 且k≠1;(2)
且k≠1;(2)![]() 且t≠2.
且t≠2.
【解析】
(1)①先确定出点C的横坐标的范围即可得出结论;
②先确定出分界点点P,P'的坐标,即可得出结论;
(2)表示出点D的坐标,再分点E在线段AD和BD上,求出AE,利用0≤AE≤2t,且AE≠t,即可得出结论.
解:(1)当t=2时,点B的坐标为(4,0),
∵点D是AB的中点,∴D(2,0),
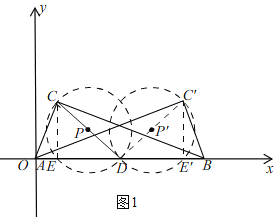
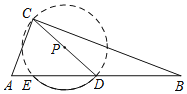
①如图1,
过点C作CE⊥AB于E,则∠CED=90°,
∴CE⊥AB,
即点C和点E的横坐标相同,
∵点E是以CD为直径与边AB的交点,
∴0≤AE≤4,
∵点E与点D重合,
∴AE≠2,
∴点E的横坐标大于等于0小于等于4,且不等于2,
即点E的横坐标大于等于0小于等于4,且不等于2,
∵点C1(﹣3,2),C2(0,2![]() ),C3(2,4),C4(4,2),
),C3(2,4),C4(4,2),
∴只有点C2,C4的横坐标满足条件,
故答案为C2,C4;
②∵△ABC的中线CD=4,
∴点C在以点D为圆心4为直径的弧上,
由①知,点C的横坐标大于等于0小于等于4,且不等于2,
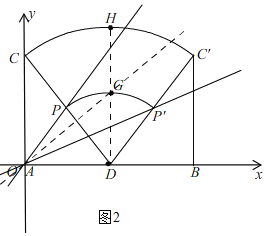
∴点C在如图2所示的![]() 上(点H(2,4)除外),
上(点H(2,4)除外),
∵点P是以CD为直径的圆的圆心,
∴点P在如图2所示的![]() 上(点G(2,2)除外),
上(点G(2,2)除外),
在Rt△OAM中,AD=2,MD=4,
根据勾股定理得,AO=2![]() ,
,
∴C(0,2![]() ),
),
同理:C'(4,2![]() ),
),
∵点P是DC的中点,
∴P(1,![]() ),
),
同理:点P'(3,![]() ),
),
当直线y=kx过点P(1,![]() )时,得k=
)时,得k=![]() ,
,
当直线y=kx过点P'(3,![]() )时,得
)时,得![]() ,
,
当直线y=kx过点G(2,2)时,得k=1,
结合图形,可得k的取值范围是![]() 且k≠1;
且k≠1;
(2)同(1)①知,点E的横坐标大于等于0小于等于2t,且不等于t,
∵点D是AB的中点,且B(2t,0),
∴D(t,0),
当点E在线段AD上时,AE=t﹣2(t﹣2)=﹣t+4≥0,
∴t≤4,
当点E在线段BE上时,AE=2(2﹣t)+t≤2t,
∴t≥![]() ,
,
∴![]() 且t≠2.
且t≠2.