ЬтФПФкШн
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=BCЃЌжБЯпMNОЙ§ЕуCЃЌЧвADЁЭMNгкDЃЌBEЁЭMNгкEЃЎ
ЃЈ1ЃЉЕБжБЯпMNШЦЕуCа§зЊЕНЭМ1ЕФЮЛжУЪБЃЌЧѓжЄЃКЂйЁїADCЁеЁїCEBЃЛЂкDE=AD+BEЃЛ
ЃЈ2ЃЉЕБжБЯпMNШЦЕуCа§зЊЕНЭМ2ЕФЮЛжУЪБЃЌЧѓжЄЃКDE=ADЉBEЃЛ
ЃЈ3ЃЉЕБжБЯпMNШЦЕуCа§зЊЕНЭМ3ЕФЮЛжУЪБЃЌЪдЮЪDEЁЂADЁЂBEОпгадѕбљЕФЕШСПЙиЯЕЃПЧыаДГіетИіЕШСПЙиЯЕЃЌВЂМгвджЄУїЃЎ

ЁОД№АИЁПЃЈ1ЃЉЂйжЄУїМћНтЮіЃЛЂкжЄУїМћНтЮіЃЛЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉDE=BEЉADЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЭЌНЧЕФгрНЧЯрЕШЕУЕНЁЯACD=ЁЯCBEЃЌМДПЩжЄУїЁїADCЁеЁїCEBЃЛ
ЃЈ2ЃЉИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНAD=CEЃЌDC=EBЃЌМДПЩжЄУїDE=ADЉBEЃЛ
ЃЈ3ЃЉгыЃЈ1ЃЉЕФжЄУїЗНЗЈРрЫЦЃЌжЄЕФЁїADCЁеЁїCEBЃЌЕУГіAD=CEЃЌDC=EBЃЌМДПЩЕУГіDEЁЂADЁЂBEЕФЕШСПЙиМќ.
ЃЈ1ЃЉЁпЁЯACB=90Ёу
ЁрЁЯACD+ЁЯBCE=90Ёу
гжЁпADЁЭMNЃЌBEЁЭMN
ЁрЁЯADC=ЁЯCEB=90Ёу
ЁрЁЯBCE+ЁЯCBE=90Ёу
ЁрЁЯACD=ЁЯCBE
дкЁїADCКЭЁїCEBжаЃЌ
ЁрЁїADCЁеЁїCEB
ЁрAD=CEЃЌDC=BE
ЁрDE=DC+CE=BE+ADЃЛ
ЃЈ2ЃЉдкЁїADCКЭЁїCEBжаЃЌ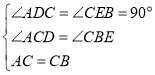
ЁрЁїADCЁеЁїCEB
ЁрAD=CEЃЌDC=EB
ЁрDE=CEЉDC=ADЉEBЃЛ
ЃЈ3ЃЉDE=BEЉADЃЎ
дкЁїADCКЭЁїCEBжаЃЌ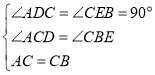
ЁрЁїADCЁеЁїCEB
ЁрAD=CEЃЌDC=BE
ЁрDE=DCЉCE=BEЉADЃЎ

ЁОЬтФПЁПЫожнЪаИпаТЧјФГЕчзгЕчТЗАхГЇЕНАВЛеДѓбЇДг2018ФъгІНьБЯвЕЩњжаеаЦИЙЋЫОжАдБЃЌЖдгІЦИепЕФзЈвЕжЊЪЖЁЂгЂгяЫЎЦНЁЂВЮМгЩчЛсЪЕМљгыЩчЭХЛюЖЏЕШШ§ЯюНјааВтЪдЛђГЩЙћШЯЖЈЃЌШ§ЯюЕФЕУЗжТњЗжЖМЮЊ100ЗжЃЌШ§ЯюЕФЗжЪ§ЗжБ№АД5ЁУ3ЁУ2ЕФБШР§МЧШыУПШЫЕФзюКѓзмЗжЃЌга4ЮЛгІЦИепЕФЕУЗжШчЯТБэЫљЪОЃЎ
| зЈвЕжЊЪЖ | гЂгяЫЎЦН | ВЮМгЩчЛсЪЕМљгы ЩчЭХЛюЖЏЕШ |
Мз | 85 | 85 | 90 |
вв | 85 | 85 | 70 |
Бћ | 80 | 90 | 70 |
ЖЁ | 90 | 90 | 50 |
ЃЈ1ЃЉЗжБ№ЫуГі4ЮЛгІЦИепЕФзмЗжЃЛ
ЃЈ2ЃЉБэжаЫФШЫЁАзЈвЕжЊЪЖЁБЕФЦНОљЗжЮЊ85ЗжЃЌЗНВюЮЊ12.5ЃЌЫФШЫЁАгЂгяЫЎЦНЁБЕФЦНОљЗжЮЊ87.5ЗжЃЌЗНВюЮЊ6.25ЃЌЧыФуЧѓГіЫФШЫЁАВЮМгЩчЛсЪЕМљгыЩчЭХЛюЖЏЕШЁБЕФЦНОљЗжМАЗНВюЃЛ
ЃЈ3ЃЉЗжЮіЃЈ1ЃЉКЭЃЈ2ЃЉжаЕФгаЙиЪ§ОнЃЌФуЖдДѓбЇЩњгІЦИепгаКЮНЈвщЃП




