Question

【题目】已知等边△ABC和等边△DBE，点D始终在射线AC上运动．

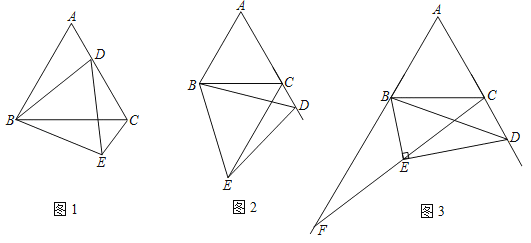
（1）如图1，当点D在AC边上时，连接CE，求证：AD＝CE；

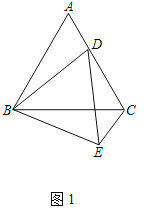
（2）如图2，当点D不在AC边上而在AC边的延长线上时，连接CE，（1）中的结论是否成立，并给予证明．

（3）如图3，当点D不在AC边上而在AC边的延长线上时，如果以BD为斜边作Rt△BDE，且∠BDE＝30°，连接CE并延长，与AB的延长线交于F点，求证：AD＝BF．

Answer 1

【答案】（1）见解析；（2）（1）中的结论成立，证明见解析；（3）见解析.

【解析】

（1）欲证明AD=CE，只要证明△ABD≌△CBE即可．
（2）如图2中，倍长BE到H，连CH，DH．首先证明△DBH是等边三角形，由（1）可知，△ABD≌△CBH，推出AD=CH，∠A=∠HCB=∠ABC=60°，推出BF∥CH，推出∠F=∠ECH，再证明△EBF≌△EHC，推出BF=CH，由此即可证明．
（3）如图2中，倍长BE到H，连CH，DH．利用（1）中结论可得AD=CH，再证明BF=CH即可解决问题．

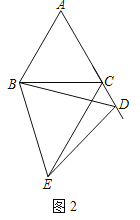
（1）证明：如图1中，

∵△ABC，△BDE都是等边三角形，

∴AB＝BC，BD＝BE，∠ABC＝∠DBE＝60°，

∴∠ABD＝∠CBE，

在△ABD和△CBE中，

，

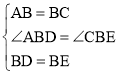∴△ABD≌△CBE（SAS），

∴AD＝CE．

（2）如图2中，

∵△ABC，△BDE都是等边三角形，

∴AB＝BC，BD＝BE，∠ABC＝∠DBE＝60°，

∴∠ABD＝∠CBE，

在△ABD和△CBE中，

，

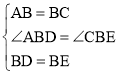∴△ABD≌△CBE（SAS），

∴AD＝CE．

（3）如图2中，倍长BE到H，连CH，DH．

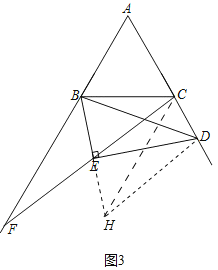
∵BE＝EH，DE⊥BH，

∴DB＝DH，∠BDE＝∠HDE＝30°，

∴∠BDH＝60°，

∴△DBH是等边三角形，

由（1）可知，△ABD≌△CBH，

∴AD＝CH，∠A＝∠HCB＝∠ABC＝60°，

∴BF∥CH，

∴∠F＝∠ECH，

在△EBF和△EHC中，

，

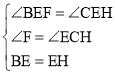∴△EBF≌△EHC（AAS），

∴BF＝CH，

∴AD＝BF．