题目内容
【题目】一张宽为6cm的平行四边形纸带ABCD如图1所示,AB=10cm,小明用这张纸带将底面周长为10cm直三棱柱纸盒的侧面进行包贴(要求包贴时没有重叠部分).小明通过操作后发现此类包贴问题可将直三棱柱的侧面展开进行分析.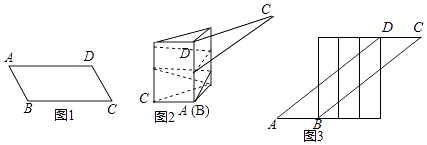
(1)若纸带在侧面缠绕三圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则纸带AD的长度为 cm;
(2)若AD=100cm,纸带在侧面缠绕多圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则这个直三棱柱纸盒的高度是 cm.
【答案】
(1)25
(2)60
【解析】解:(1)易得AF=DF,FB=DH,过点B作BI⊥AD,垂足为I,
设AF=x,则HF=FB= ![]() =
= ![]() x,
x,
在直角△BEH中,由勾股定理得到:( ![]() x)2+102=x2,
x)2+102=x2,
解得x= ![]() ,
,
则AD=2x=25.
故答案是:25;(2)直三棱柱的侧面积等于平行四边形ABCD的面积,则直三棱柱的高h= ![]() =60(cm),
=60(cm),
故答案是:60.

(1)由题意可知直三棱柱的侧面积等于平行四边形ABCD的面积,则易得AF=DF,FB=DH,可设AF=x,运用等积法求出BF,从而由勾股定理构造方程求得x的值即可;
(2)直三棱柱的侧面积等于平行四边形ABCD的面积.

练习册系列答案
相关题目