Question

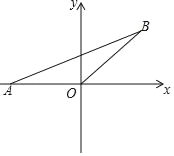
【题目】如图，等腰△AOB中，AO＝BO＝2，点A在x轴上，OB与x轴的夹角为45°；

(1)求直线AB、OB的解析式；

(2)若将△AOB沿着x轴翻折再向右平移两个单位求直线AB的解析式．

Answer 1

【答案】(1)直线AB的解析式为：y＝（﹣1）x+2+1，直线OB的解析式为y＝x；(2)y＝﹣（1+）x．

【解析】

（1）过B作BC⊥x轴于C，根据已知条件得到BC=OC，求得A（-2，0），B（，），解方程组即可得到结论；

（2）根据折叠的性质得到点B的对称点为B′（，-），向右平移两个单位，得到点A的对称点为A′（0，0），点B′的对称点B″（+2，-），解方程组即可得到结论．

(1)过B作BC⊥x轴于c，

∵∠BOC＝45°，

∴BC＝OC，

∵AO＝BO＝2，

∴BC＝OC＝，

∴A（﹣2，0），B（，），

设直线AB的解析式为：y＝kx+b，

∴，

解得：，

∴直线AB的解析式为：y＝（﹣1）x+2+1，

设直线OB的解析式为y＝mx，

∴＝m，

∴m＝1，

∴直线OB的解析式为y＝x；

(2)∵将△AOB沿着x轴翻折，

∴点B的对称点为B′（，﹣），

∵再向右平移两个单位，

∴点A的对称点为A′（0，0），点B′的对称点B″（+2，﹣），

设平移后的直线的解析式为：y＝ax，

∴﹣＝（+2）a，

∴a＝﹣（1+），

∴将△AOB沿着x轴翻折再向右平移两个单位求直线AB的解析式为y＝﹣（1+）x．