题目内容
【题目】如图，抛物线y1= 
（x+1）2+1与y2=a（x﹣4）2﹣3交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于B、C两点，且D、E分别为顶点．则下列结论：①a= 
；②AC=AE；③△ABD是等腰直角三角形；④当x＞1时，y1＞y2.其中正确结论的个数是（ ）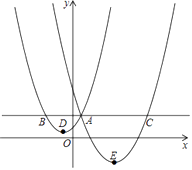
A.1个
B.2个
C.3个
D.4个
【答案】B
【解析】解： ∵抛物线 
与 
交于点A（1，3），∴3=a（1﹣4）2﹣3，解得：a= 
，故①正确；
∵E是抛物线的顶点，
∴AE=EC，∴无法得出AC=AE，故②错误；
当y=3时，3= 
，解得：x1=1，x2=﹣3，
故B（﹣3，3），D（﹣1，1），则AB=4，AD=BD= 
，
∴AD2+BD2=AB2，
∴③△ABD是等腰直角三角形，正确；
∵ = 
时，解得：x1=1，x2=37，
∴当37＞x＞1时，y1＞y2，故④错误．
所以答案是：B．
练习册系列答案
相关题目
【题目】学校计划在七年级学生中开设4个信息技术应用兴趣班，分别为“无人机”班，“3D打印”班，“网页设计”班，“电脑绘画”班，规定每人最多参加一个班，自愿报名．根据报名情况绘制了下面统计图表， 
请回答下列问题：
七年级兴趣班报名情况统计表．
兴趣班名称 | 频率 |
“无人机” | a |
“3D打印” | 0.05 |
“网页设计” | 0.25 |
“电脑绘画” | 0.40 |
（1）报名参加兴趣班的总人数为人；统计表中的a=；
（2）将统计图补充完整；
（3）为了均衡班级人数，在“电脑绘画”班中至少动员几人到“3D打印”班，才能使“电脑绘画”班人数不超过“3D打印”班人数的2倍？
