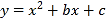题目内容
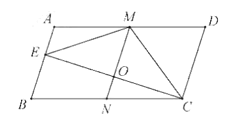
【题目】如图，平行四边形ABCD中，
于点E，CE的垂真平分线MV分别交AD、BC于M、N，交CE于O，连接CM、EM，下列结论：（1）
（2）
（3）
（4）
·其中正确的个数有（ ）
A.1个B.2个C.3个D.4个
【答案】C
【解析】
①由平行四边形性质可得AB∥CD，由线段垂直平分线性质可得ME=MC，再根据等角的余角相等可得①正确；②构造△AME≌△DMG（ASA），即可证明②正确；③利用平行四边形性质、线段垂直平分线性质和AD=2AB可得四边形CDMN是菱形，依据菱形性质即可证明③正确；④S△CDM=
S菱形CDMN，S四边形BEON＜
S菱形CDMN，④不一定成立；
解：延长EM交CD的延长线于G，如图，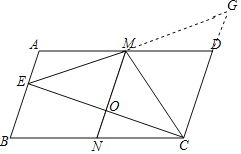
∵ABCD是平行四边形，
∴AB∥CD
∴∠AEM=∠G
∵CE⊥AB
∴CE⊥CD
∵MN垂直平分CE，
∴ME=MC
∴∠MEC=∠MCE
∵∠MEC+∠G=90°，∠MCE+∠DCM=90°
∴∠DCM=∠G
∴∠AEM=∠DCM
故①正确；
∵∠DCM=∠G
∴MC=MG
∴ME=MG
∵∠AME=∠DMG
∴△AME≌△DMG（ASA）
∴AM=DM
故②正确；
∵ABCD是平行四边形，
∴AB∥CD，AB=CD，AD∥BC，AD=BC
∵CE⊥AB，MN⊥CE
∴AB∥MN∥CD
∴四边形ABNM、四边形CDMN均为平行四边形
∴MN=AB
∵AM=MD=AD，AD=2AB
∴MD=CD=MN=NC
∴四边形CDMN是菱形
∴∠BCD=2∠DCM，
故③正确；
设菱形ABNM的高为h，则S△CDM=S菱形CDMN，S四边形BEON=（BE+ON）×h=
ON×h
∵OM=（AE+CD）
∴CD＜OM＜AB
∴ON＜CD
∴S四边形BEON＜CD×h=S菱形CDMN，
故④不一定成立；
故选：C．
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
【题目】某水果批发市场规定，一次购买苹果不超过100kg（包括100kg），批发价为5元，如果一次购买100kg以上苹果，超过100kg的部分苹果价格打8折．
（I）请填写下表
购买量/kg | 0 | 50 | 100 | 150 | 200 | … |
付款金额/元 | 0 | 250 | _ | 700 | __ | … |
（Ⅱ）写出付款金额关于购买量的函数解析式；
（Ⅲ）如果某人付款2100元，求其购买苹果的数量．
