题目内容
【题目】已知关于x的方程![]()
(1)若方程有两个相等的实数根,求m的值,并求出此时方程的根;
(2)是否存在正数m,使方程的两个实数根的平方和等于224.若存在,求出满足条件的m的值;若不存在,请说明理由.
【答案】(1)x1=x2=﹣2.(2)不存在正数m使方程的两个实数根的平方和等于224
【解析】
(1)方程有两相等的实数根,利用△=0求出m的值.化简原方程求得方程的根.
(2)利用根与系数的关系x1+x2=-![]() , =4m-8,x1x2=
, =4m-8,x1x2=![]() =4m2,x12+x22=(x1+x2)2-2x1x2,代入即可得到关于m的方程,求出m的值,再根据△来判断所求的m的值是否满足原方程.
=4m2,x12+x22=(x1+x2)2-2x1x2,代入即可得到关于m的方程,求出m的值,再根据△来判断所求的m的值是否满足原方程.
(1)∵a=![]() ,b=﹣(m﹣2),c=m2方程有两个相等的实数根,
,b=﹣(m﹣2),c=m2方程有两个相等的实数根,
∴△=0,即△=b2﹣4ac=[﹣(m﹣2)]2﹣4×![]() ×m2=﹣4m+4=0,
×m2=﹣4m+4=0,
∴m=1.
原方程化为:![]() x2+x+1=0 x2+4x+4=0,(x+2)2=0,
x2+x+1=0 x2+4x+4=0,(x+2)2=0,
∴x1=x2=﹣2.
(2)不存在正数m使方程的两个实数根的平方和等于224.
∵x1+x2=﹣![]() =4m﹣8,x1x2=
=4m﹣8,x1x2=![]() =4m2x12+x22=(x1+x2)2﹣2x1x2=(4m﹣8)2﹣2×4m2=8m2﹣64m+64=224,
=4m2x12+x22=(x1+x2)2﹣2x1x2=(4m﹣8)2﹣2×4m2=8m2﹣64m+64=224,
即:8m2﹣64m﹣160=0,
解得:m1=10,m2=﹣2(不合题意,舍去),
又∵m1=10时,△=﹣4m+4=﹣36<0,此时方程无实数根,
∴不存在正数m使方程的两个实数根的平方和等于224.

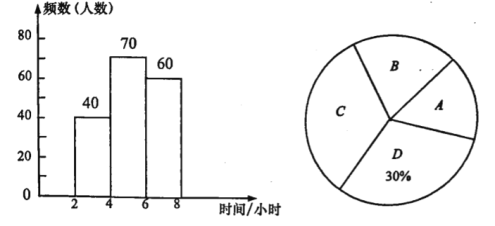
【题目】为弘扬中华民族传统文化,某校举办了“燕城诗文大赛”活动,从中随机抽取部分学生的比赛成绩,根据成绩(成绩都高于50分),绘制了如下的统计图表(不完整):
组别 | 分数 | 人数 |
第1组 |
| 16 |
第2组 |
|
|
第3组 |
| 20 |
第4组 |
|
|
第5组 |
| 6 |
请根据以上信息,解答下列问题:
(1)此次随机抽取的学生数是 人,![]() ,
,![]() ;
;
(2)计算扇形统计图中“第5组”所在扇形圆心角的度数;
(3)若该校共有1500名学生,那么成绩低于70分的约有多少人?

【题目】银川九中要举办“不忘初心跟党走”2018年元旦合唱比赛,为迎接比赛,某校区七年级(3)(4)班决定订购同一套服装,两班一共有103人(三班人数多于四班),经协商,某服装店给出的价格如下:
购买人数/人 | 1~50人 | 50~100人 | 100以上人 |
每套服装价格/元 | 50 | 45 | 40 |
(1)如果两个班都以班为单位分别购买,则一共需花费4875元,那么三、四班各有多少名学生?
(2)如果两个班联合起来,做为一个整体购买,则能节省多少元钱?
(3)该服装店此次出售的服装每套成本是32元,如果按上面的第(2)问形式购买,请计算这个服装店此次出售服装的利润率是多少?