题目内容
【题目】如图1，在
中，
，
是两条外角平分线.
（1）求证：
.
（2）如图2，
是由的外角平分线围成的三角形.求证：一定是锐角三角形.
【答案】（1）证明见解析；（2）证明见解析．
【解析】
（1）如图1，根据角平分线的定义得到∠3=
∠CBE，∠4=∠FCB．由三角形外角和为360°得到∠CBE+∠FCB=180°+∠A，从而得到∠3+∠4=90°+∠A．在△BDC中，由三角形内角和定理即可得到结论；
（2）如图2，根据角平分线定义得∠1=∠2，∠3=∠4，再利用三角形外角性质得∠1+∠2=∠BAC+∠ACB=∠BAC+180°﹣∠3﹣∠4，则∠1+∠3=90°+∠BAC，然后根据三角形内角和定理得到∠D=180°﹣（∠1+∠3）=90°﹣∠BAC，于是可判断∠D为锐角，同理可得∠F=90°﹣∠ACB，∠E=90°﹣∠ABC，也可判断∠E、∠F都是锐角，所以△DEF为锐角三角形．
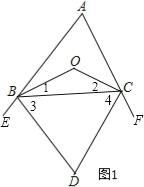
（1）如图1．
∵BD平分∠CBE，∴∠3=∠CBE．
∵CD平分∠FCB，∴∠4=∠FCB．
∵∠CBE+∠FCB+180°－∠A=360°，∴∠CBE+∠FCB=180°+∠A，∴∠3+∠4=（∠CBE+∠FCB）=（180°+∠A）=90°+∠A，∴∠D=180°－（∠3+∠4）=180°-（90°+∠A）=90°∠A；
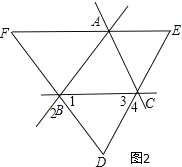
（2）如图2．
∵BD和CD为△ABC的外角平分线，∴∠1=∠2，∠3=∠4．
∵∠1+∠2=∠BAC+∠ACB=∠BAC+180°﹣∠3﹣∠4，∴2∠1=∠BAC+180°﹣2∠3，∴∠1+∠3=90°+∠BAC，∴∠D=180°﹣（∠1+∠3）=90°﹣∠BAC，∴∠D为锐角，同理可得∠F=90°﹣∠ACB，∠E=90°﹣∠ABC，∴∠E、∠F都是锐角，∴△DEF为锐角三角形．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
