题目内容
【题目】如图,将一副三角板中含有30°角的三角板的直角顶点落在等腰直角三角形的斜边的中点D处,并绕点D旋转,两直角三角板的两直角边分别交于点E,F,下列结论:①DE=DF;②S四边形AEDF=S△BED+S△CFD;③S△ABC=EF2;④EF2=BE2+CF2,其中正确的序号是_____.

【答案】①②④.
【解析】
连接AD,如图,由已知条件利用ASA推导证明△DBE≌△DAF,根据全等三角形的性质可得DE=DF,由此可判断①;同①一样的道理可证明△DCF≌△DAE,由此可判断②;由S△ABC=![]() ADBC=
ADBC=![]() AD2AD=AD2,确定出只有当DE⊥AB时,四边形AEDF为矩形,此时AD=EF,由此可以判断③;在Rt△AEF中,EF2=AE2+AF2,再根据△DBE≌△DAF,△DCF≌△DAE,即可得到EF2=BE2+CF2,由此可判断④.
AD2AD=AD2,确定出只有当DE⊥AB时,四边形AEDF为矩形,此时AD=EF,由此可以判断③;在Rt△AEF中,EF2=AE2+AF2,再根据△DBE≌△DAF,△DCF≌△DAE,即可得到EF2=BE2+CF2,由此可判断④.
连接AD,如图,
∵△ABC为等腰直角三角形,
∴AB=AC,∠B=∠C=45°,
∵点D为等腰直角△ABC的斜边的中点,
∴AD⊥BC,BD=CD=AD,AD平分∠BAC,
∴∠2+∠3=90°,∠1=45°,
∵∠EDF=90°,即∠4+∠3=90°,
∴∠2=∠4,
在△DBE和△DAF中
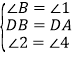 ,
,
∴△DBE≌△DAF(ASA),
∴DE=DF,所以①正确;
同理可得△DCF≌△DAE,
∴S四边形AEDF=S△BED+S△CFD,所以②正确;
∵S△ABC=![]() ADBC=
ADBC=![]() AD2AD=AD2,
AD2AD=AD2,
而只有当DE⊥AB时,四边形AEDF为矩形,此时AD=EF,
∴S△ABC不一定等于EF2,所以③错误;
在Rt△AEF中,EF2=AE2+AF2,
∵△DBE≌△DAF,△DCF≌△DAE,
∴BE=AF,CF=AE,
∴EF2=BE2+CF2,所以④正确,
故答案为:①②④.