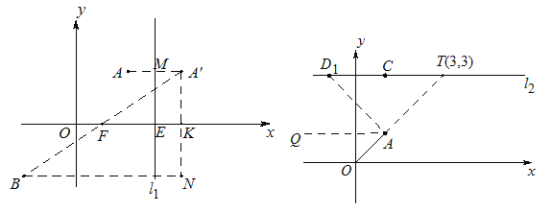题目内容
【题目】在平面直角坐标系中，点A(a,1)、B(－1,b)的坐标满足：
.
(1)直接写出点A、B的坐标；
(2)如图，过点E(m,0)(m>1)作x轴的垂线l1,点A关于l1的对称点为A’(2m-1,1),若BA’交x轴于点F，当E点在x轴上运动时，求EF的长度;
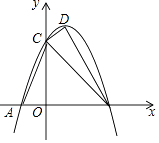
(3)如图，把点A向上平移2个单位到点C,过点C作y轴的垂线l2,点D(n,c)在直线l2上(不和C重合),若∠CDA=
,连接OA、DA,∠AOx=45°，若满足∠DAO=225°－，求n的取值范围.
【答案】（1）A(1，1)，B(－1，－1)；（2）1；（3）1＜n≤3
【解析】
（1）由非负数的性质可求得a、b的值，可求得A、B的坐标；
（2）设A与A′的连线交l1于M，F(a，0)过A′作x轴垂线，B作y轴垂线交于N，A′N交x轴于K，根据△A’BN的面积列方程求解即可得a的值，进而求得EF的长度；
（3）OA交l2于T，先求出T的坐标，分情况讨论即可求解.
解：（1）由题意得，a-1=0,a+b=0,
解得：a=1,b=-1，
∴A(1，1)，B(－1，－1)
（2）解：设A与A′的连线交l1于M，∵A′(2m－1，1)
设F(a，0)过A′作x轴垂线，B作y轴垂线交于N，A′N交x轴于K
∴FK=2m－1－a
S△A′FK=
×1×(2m－1－a)
SFBNK=×1×(2m－1－a+2m)
S△A′BN=×2×2 m
∴×1×(2m－1－a)+×1×(2m－1－a+2m)=×2×2m
∴2m－1－a+4m－1－a=4m
∴a=m－1
∴F(m－1，0) ∴EF=m－(m－1)=1；
（3）C(1，3)，OA交l2于T
∵A(1，1) ∴OA为一、三象限角分线
∴T的横纵坐标相等 ∴T(3，3)
（Ⅰ）D在C的左侧时n＜1时
过A作AQ∥l2 ∴∠DAO=45+α
（Ⅱ）D在C的后侧，T的左侧时 1＜n＜3
∠DAO=180－α+45=225°－α
（Ⅲ）D与T重合时，∠DAO=180°=225°－45°满足题义
（Ⅳ）D在T的右侧时 ∠DAO=135°+α
∴综上所述：1＜n≤3.
故答案为：（1）A(1，1)，B(－1，－1)；（2）1；（3）1＜n≤3.
