��Ŀ����
����Ŀ����ͼ��������y=��x2+��m+2��x+ ![]() ��x�ύ��A����2��n��0����B��4+n��0�����㣨A��B����ࣩ����y�ύ�ڵ�C������ΪD��
��x�ύ��A����2��n��0����B��4+n��0�����㣨A��B����ࣩ����y�ύ�ڵ�C������ΪD��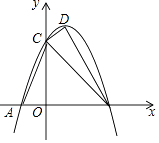
��1����������ߵĽ���ʽ��
��2���Ե�BΪֱ�Ƕ�����ֱ��������BCE��б��CE�������߽��ڵ�P����CP=EP�����P�����ꣻ
��3������BOC�������Ķ���B˳ʱ���ڵ�һ��������ת����ת�ĽǶ�Ϊ������ת���ͼ��Ϊ��BO��C�䣮����ת��ġ�BO��C����һ����BD�غ�ʱ�����BO��C�䲻��BD�ϵĶ�������꣮
���𰸡�
��1���⣺�����⩁2��n+4+n=m+2��
���m=0��
��y=��x2+2x+3
��2���⣺��ͼ1�У���P��m����m2+2m+3������֪A����1��0����B��3��0����C��0��3����

��PC=PE����CBE=90�㣬
��PB=PC=PE��
��m2+����m2+2m+3��3��2=��m��3��2+����m2+2m+3��2��
�����ã�m2��m��3=0��
��m= ![]() ��
��
��P�� ![]() ��
�� ![]() ����P��
����P�� ![]() ��
�� ![]() ��
��
��3���⣺��ͼ2�У���BC����BP�غ�ʱ������O����O��D��OB��D��

��Ϊ��PBC+��CBO��=��CBO��+��ABO��=45�㣬
���ԡ�ABO��=��PBC��
���DBO��ס�CBP��
���� ![]() =
= ![]() ��
��
���� ![]() =
= ![]() ��
��
����BD=3O��D��
��O��D=x����BD=3x�����ݹ��ɶ�������x2+��3x��2=32��
���x= ![]() ��
��
����BD= ![]() ��
��
���Ե�O�������Ϊ��3�� ![]() ��
�� ![]() ����
����
��ͼ3�У���BO����BP�غ�ʱ������B��x��Ĵ���BE������C����C��E��BE��E��
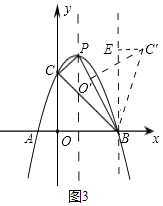
��Ϊ��PBE+��EBC��=��PBE+��CBP=45�㣬
���ԡ�EBC��=��PBC��
���ԡ�EBC��ס�CBP��
���� ![]() =
= ![]() ��
��
���� ![]() =
= ![]() ��
��
����BE=3C��E��
��C��EΪy����BE=3y�����ݹ��ɶ�����
��y2+��3y��2=��3 ![]() ��2��
��2��
���y= ![]() ��
��
����BE= ![]() ��
��
����C���������3+ ![]() ��
�� ![]() ��
��
����������1�����ø���ϵ���Ĺ�ϵ����������ߵĶԳ���x=-![]() =
=![]() ��x1+x2����������x1��x2����������x��������ĺ����꣬�г��������m���ɽ�����⡣
��x1+x2����������x1��x2����������x��������ĺ����꣬�г��������m���ɽ�����⡣
��2���ȸ��ݺ�������ʽ���A��B��C�������꣬��P��m��-m2+2m+3������֤��PC=PB�������������빫ʽ���г����̼��ɽ�����⡣
��3��Ӧ������������ǣ���BC����BP�غϣ���ʱO��Ϊ����㣮����O����O��D��OB��D�����ݵ�B��C������֤�á�CBO=��C��BO��=45�㣬�������Ƚ�ͬʱ��ȥ��CBO���ɵõ���PBC=��O��BD������֤�á�PBC�ס�O��BD������PC��BC�ı�����ϵ�������O��D��BD�ı�����ϵ���������ɹ��ɶ�����O��B����OB���ij����O��D��BD�ij������ɵõ���O������ꣻ
��BO����BP�غ�ʱ��C��Ϊ����ĵ㣮�ɹ�B��ֱ��BE��x�ᣬ��C����C��E��BE��E������1����˼·����֤��EBC��ס�CBP��ͬ���ܵõ�C��E��BE�ı�����ϵ�������ɹ��ɶ������������߶εij������ɵõ���C������ꡣ
�����㾫�������ո���ϵ���Ĺ�ϵ���ɶ����ĸ����ǽ����ĸ�������Ҫ֪��һԪ���η���ax2+bx+c=0��a��0���ĸ��ɷ��̵�ϵ��a��b��c����������֮�͵��ڷ��̵�һ����ϵ�����Զ�����ϵ�����õ��̵��෴��������֮�����ڳ�������Զ�����ϵ�����õ��̣�ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2��

 �ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�
�ϴ�̸�������������νӽ̳��Ͼ���ѧ������ϵ�д�����Ŀ�����й�������д��ᡱ�����������̨�����������ֹ���ίԱ����������Ľ�Ŀ��ϣ��ͨ����Ŀ�IJ�����������������˹�ע�Ժ����Ļ���ѧϰ��ijУҲ��չ��һ�Ρ�������д��������ÿλ����ѧ����д40�����֣����������������ȡ����ѧ������д���������д��ȷ�ĺ��ָ���x���Ƴ������²�������ͳ��ͼ��

����������Ϣ�ش��������⣺
��1�����ι������ȡ���� ����ѧ�����е��飬��д��ȷ�ĺ��ָ���x���� ����Χ��������ࣻ
��2����ȫƵ���ֲ�ֱ��ͼ��
��3�����������ֵ���±���ʾ�����ø��������ֵ��������ÿλѧ����д��ȷ�ĺ��ָ���������ѧ����д��ȷ�ĺ��ָ�����ƽ������
��д��ȷ�ĺ��ָ���x | ����ֵ |
1��x��11 | 6 |
11��x��21 | 16 |
21��x��31 | 26 |
31��x��41 | 36 |
��4����У����1350��ѧ���������д��ȷ�ĺ��ָ���������21����Ϊ���ã�������Ƹ�У���Ρ�������д�������ﵽ���õ�ѧ��������