题目内容
【题目】如图，将一张等边三角形纸片沿中位线剪成4个小三角形，称为第一次操作：然后，将其中的一个三角形按同样方式再剪成4个小三角形，共得到7个小三角形，称为第二次操作；再将其中一个三角形按同样方式再剪成4个小三角形，共得到10个小三角形，称为第三次操作；…根据以上操作，①第七次操作共得到个三角形；②若要得到220个小三角形，则需要操作的次数是 ．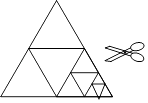 
【答案】22；73
【解析】解：∵第一次操作后，三角形共有4个；
第二次操作后，三角形共有4+3=7个；
第三次操作后，三角形共有4+3+3=10个；
…
第n次操作后，三角形共有4+3（n﹣1）=3n+1个；
所以第七次操作后小三角形个数是3×7+1=22个，
当得到220个小三角形时，3n+1=220，则n=73．
故答案是：22；73．
【考点精析】解答此题的关键在于理解数与式的规律的相关知识，掌握先从图形上寻找规律，然后验证规律，应用规律，即数形结合寻找规律，以及对等边三角形的性质的理解，了解等边三角形的三个角都相等并且每个角都是60°．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】“中国汉字听写大会”是由中央电视台和国家语言文字工作委员会联合主办的节目，希望通过节目的播出，能吸引更多的人关注对汉字文化的学习．某校也开展了一次“汉字听写”比赛，每位参赛学生听写40个汉字．比赛结束后随机抽取部分学生的听写结果，按听写正确的汉字个数x绘制成了以下不完整的统计图．
根据以上信息回答下列问题：
（1）本次共随机抽取了 名学生进行调查，听写正确的汉字个数x在 范围的人数最多；
（2）补全频数分布直方图；
（3）各组的组中值如下表所示．若用各组的组中值代表各组每位学生听写正确的汉字个数，求被调查学生听写正确的汉字个数的平均数；
听写正确的汉字个数x | 组中值 |
1≤x＜11 | 6 |
11≤x＜21 | 16 |
21≤x＜31 | 26 |
31≤x＜41 | 36 |
（4）该校共有1350名学生，如果听写正确的汉字个数不少于21个定为良好，请你估计该校本次“汉字听写”比赛达到良好的学生人数．
