题目内容
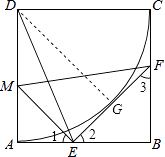
【题目】如图，在边长为2的正方形ABCD中，以点D为圆心、DC为半径作 
，点E在AB上，且与A、B两点均不重合，点M在AD上，且ME=MD，过点E作EF⊥ME，交BC于点F，连接DE、MF．
（1）求证：EF是 所在⊙D的切线；
（2）当MA= 
时，求MF的长；
（3）试探究：△MFE能否是等腰直角三角形？若是，请直接写出MF的长度；若不是，请说明理由．
【答案】
（1）
证明：过点D作DG⊥EF于G，
∵ME=MD，
∴∠MDE=∠MED，
∵EF⊥ME，
∴∠DEM+∠GED=90°，
∵∠DAB=90°，
∴∠MDE+∠AED=90°，
∴∠AED=∠GED，
∵在△ADE和△GDE中，
，
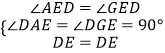∴△ADE≌△GDE（AAS），
∴AD=GD，
∵ 
的半径为DC，即AD的长度，
∴EF是 所在⊙D的切线；
（2）
MA= 
时，ME=MD=2﹣ = 
，
在Rt△AME中，AE= 
= 
=1，
∴BE=AB﹣AE=2﹣1=1，
∵EF⊥ME，
∴∠1+∠2=180°﹣90°=90°，
∵∠B=90°，
∴∠2+∠3=90°，
∴∠1=∠3，
又∵∠DAB=∠B=90°，
∴△AME∽△BEF，
∴ 
，
即 
，
解得EF= 
，
在Rt△MEF中，MF= 
；
（3）
假设△MFE能是等腰直角三角形，
则ME=EF，
∵在△AME和△BEF中，
，
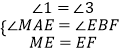∴△AME≌△BEF（AAS），
∴MA=BE，
设AM=BE=x，
则MD=AD﹣MA=2﹣x，AE=AB﹣BE=2﹣x，
∵ME=MD，
∴ME=2﹣x，
∴ME=AE，
∵ME、AE分别是Rt△AME的斜边与直角边，
∴ME≠AE，
∴假设不成立，
故△MFE不能是等腰直角三角形．
【解析】（1）过点D作DG⊥EF于G，根据等边对等角可得∠MDE=∠MED，然后根据等角的余角相等求出∠AED=∠GED，再利用“角角边”证明△ADE和△GDE全等，根据全等三角形对应边相等可得AD=GD，再根据切线的定义即可得证；（2）求出ME=MD= ，然后利用勾股定理列式求出AE，再求出BE，根据同角的余角相等求出∠1=∠3，然后求出△AME和△BEF相似，根据相似三角形对应边成比例列式求出EF，再利用勾股定理列式计算即可得解；（3）假设△MFE能是等腰直角三角形，根据等腰直角三角形的性质可得ME=EF，先利用“角角边”证明△AME和△BEF全等，根据全等三角形对边角相等可得AM=BE，设AM=BE=x，然后表示出MD，AE，再根据ME=MD，从而得到ME=AE，根据直角三角形斜边大于直角边可知△MEF不可能是等腰直角三角形．
