��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�ΪA����4��3����B����3��1����C����1��3����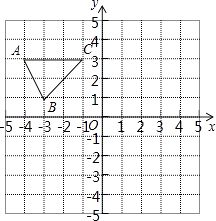
��1���밴����Ҫ��ͼ��
�ٽ���ABC������ƽ��4����λ���ȡ�������ƽ��2����λ���ȣ��õ���A1B1C1 �� ������A1B1C1��
�ڡ�A2B2C2���ABC����ԭ��O�����ĶԳƣ�������A2B2C2 ��
��2���ڣ�1�������õġ�A1B1C1�͡�A2B2C2���ڵ�M�����ĶԳƣ���ֱ��д���Գ�����M������꣮
���𰸡�
��1��
�⣺�١�A1B1C1��ͼ��ʾ��
�ڡ�A2B2C2��ͼ��ʾ��

��2��
�⣺����B1B2��C1C2���õ��Գ�����M������Ϊ��2��1����
����������1���ٸ�������ṹ�ҳ���A��B��Cƽ�ƺ�Ķ�Ӧ��A1��B1��C1��λ�ã�Ȼ��˳�����Ӽ��ɣ��ڸ�������ṹ�ҳ�A��B��C����ԭ��O�����ĶԳƵ�A2��B2��C2��λ�ã�Ȼ��˳�����Ӽ��ɣ���2������B1B2 �� C1C2 �� ������ǶԳ�����M��

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ