题目内容
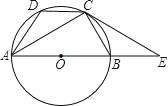
【题目】已知,如图在ABCD中,点E为AB上一点,连接CE、DE,且CE⊥AB,CE=AB,点F为BC上一点,连接DF交CE于点G,∠CGD=∠B;

(1)若CG=2,AD=3,求GE的长;
(2)若CF=![]() DE,求证:AD=CG+BE.
DE,求证:AD=CG+BE.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)求出![]() ,根据勾股定理计算即可求解;
,根据勾股定理计算即可求解;
(2)可得![]() ,根据角的和差关系可得
,根据角的和差关系可得![]() ,再根据线段的和差关系即可得证.
,再根据线段的和差关系即可得证.
解:(1)在ABCD中,
∵AB∥CD,CE⊥AB,
∴CD⊥CE,
∴∠DCE=∠CEB=90°,
∵CE=AB,
∴CE=CD,
∴△CDE是等腰三角形,
∵∠CGD=∠B,
∴△CDG≌△ECB,
∴DG=BC=AD=3,
∴CD=![]() ,
,
GE=![]() ;
;
(2)CF=![]() ,
,
∴∠CDF=∠CFD=∠BCE,∠CGD=∠BCE+∠CFD=2∠CDF,
∴∠CDF=30°,
DG=2CG,BC=2BE,CG=BE=![]() ,
,
∴AD=BC=CG+BE.
即AD=CG+BE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目