题目内容
 如图,直角梯形ABCD中,∠ADC=90°,AB=6,AD=2,BC=4,你可以在CD边上找到多少个点,使其与点A、B构成一个直角三角形
如图,直角梯形ABCD中,∠ADC=90°,AB=6,AD=2,BC=4,你可以在CD边上找到多少个点,使其与点A、B构成一个直角三角形
- A.1个
- B.2个
- C.3个
- D.无数多个
B
分析:根据直径所对的圆周角相等,此题可以转化为判断以AB为直径的圆与CD的交点个数.
根据直线和圆的位置关系与数量之间的联系:过AB的中点作CD的垂线段,根据梯形的中位线定理,得该距离=3,等于圆的半径,所以直线和圆相切,即直线CD和以AB为直径的圆有一个交点,则构成直角三角形的有一个.
解答: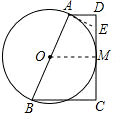 解:设AB的中点为O,过O作OM∥AD交CD于M,
解:设AB的中点为O,过O作OM∥AD交CD于M,
则OM是直角梯形ABCD的中位线,
∴OM= (AD+BC)=3;
(AD+BC)=3;
∵OM∥AD,AD⊥CD,
∴OM⊥AC;
以O为圆心,AB为直径作圆,
由于OM=3= AB,且OM⊥CD,
AB,且OM⊥CD,
所以CD与⊙O相切,因此在CD上,点M符合要求,
过点A作AE⊥AB于点A,
∵∠DAB是钝角,
∴E点在CD上,
故符合条件的点有两个,即点E、点M.
故选B.
点评:本题考查了圆周角定理的应用,可将问题转化为判断直线和圆的位置关系.
分析:根据直径所对的圆周角相等,此题可以转化为判断以AB为直径的圆与CD的交点个数.
根据直线和圆的位置关系与数量之间的联系:过AB的中点作CD的垂线段,根据梯形的中位线定理,得该距离=3,等于圆的半径,所以直线和圆相切,即直线CD和以AB为直径的圆有一个交点,则构成直角三角形的有一个.
解答:
 解:设AB的中点为O,过O作OM∥AD交CD于M,
解:设AB的中点为O,过O作OM∥AD交CD于M,则OM是直角梯形ABCD的中位线,
∴OM=
 (AD+BC)=3;
(AD+BC)=3;∵OM∥AD,AD⊥CD,
∴OM⊥AC;
以O为圆心,AB为直径作圆,
由于OM=3=
 AB,且OM⊥CD,
AB,且OM⊥CD,所以CD与⊙O相切,因此在CD上,点M符合要求,
过点A作AE⊥AB于点A,
∵∠DAB是钝角,
∴E点在CD上,
故符合条件的点有两个,即点E、点M.
故选B.
点评:本题考查了圆周角定理的应用,可将问题转化为判断直线和圆的位置关系.

练习册系列答案
相关题目
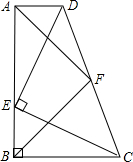 如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.
如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.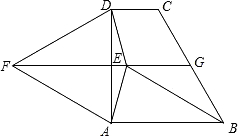 ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.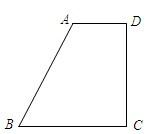 如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.
如图,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.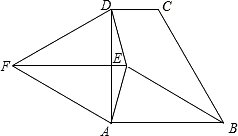 (2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.
(2013•深圳二模)如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF. 已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.
已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.