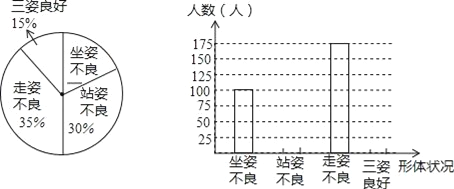
题目内容
【题目】如图:在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,有下列结论:①∠AED=∠CED;②OE=OD;③△BEH≌△HDF;④BC﹣CF=2EH;⑤AB=FH.其中正确的结论有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,有下列结论:①∠AED=∠CED;②OE=OD;③△BEH≌△HDF;④BC﹣CF=2EH;⑤AB=FH.其中正确的结论有( )
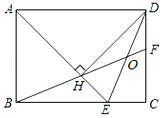
A. 5个 B. 4个 C. 3个 D. 2个
【答案】B
【解析】分析: 先证明△ABE和△ADH是等腰直角三角形,得出AD=AE,AB=AH=DH=DC,得出∠ADE=∠AED,即可得出①正确;先证出OE=OH,同理:OD=OH,得出OE=OD,②正确;由ASA证出△BEH≌△HDF,得出③正确;过H作HK⊥BC于K,可知![]() ,HK=KE,得出
,HK=KE,得出![]() ,BC=2HK+2HE=FC+2HE得出④正确.
,BC=2HK+2HE=FC+2HE得出④正确.
详解: ∵四边形ABCD是矩形,
∴![]() AB=DC,AD∥BC,
AB=DC,AD∥BC,
∴∠ADE=∠CED,
∵∠BAD的平分线交BC于点E,
∴![]()
∴△ABE和△ADH是等腰直角三角形,
∴![]()
∵![]()
∴AD=AE,AB=AH=DH=DC,
∴∠ADE=∠AED,
∴∠AED=∠CED,
∴①正确;
∵![]()
∴![]() ,
,
∵![]()
∴![]() ,
,
∴![]() ,
,
∴∠OHE=∠AED,
∴OE=OH,
同理:OD=OH,
∴OE=OD,
∴②正确;
∵![]()
∴∠HBE=∠FHD,
在△BEH和△HDF中,
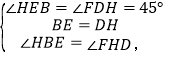
∴△BEH≌△HDF(ASA),
∴③正确;
BCCF=2HE正确,过H作HK⊥BC于K,
可知![]() ,HK=KE,
,HK=KE,
由上知HE=EC,
∴![]() ,
,
又![]() ,HE
,HE
故![]() ,BC=2HK+2HE=FC+2HE
,BC=2HK+2HE=FC+2HE
∴④正确;
⑤不正确;
故选B.

 名校课堂系列答案
名校课堂系列答案【题目】在眉山市开展城乡综合治理的活动中,需要将![]() 、
、![]() 、
、![]() 三地的垃圾50立方米、40立方米、50立方米全部运往垃圾处理场
三地的垃圾50立方米、40立方米、50立方米全部运往垃圾处理场![]() 、
、![]() 两地进行处理.已知运往
两地进行处理.已知运往![]() 地的数量比运往
地的数量比运往![]() 地的数量的2倍少10立方米.
地的数量的2倍少10立方米.
(1)求运往两地的数量各是多少立方米?
(2)若![]() 地运往
地运往![]() 地
地![]() 立方米
立方米![]() 为整数),
为整数),![]() 地运往
地运往![]() 地30立方米,
地30立方米,![]() 地运往
地运往![]() 地的数量小于
地的数量小于![]() 地运往
地运往![]() 地的2倍.其余全部运往
地的2倍.其余全部运往![]() 地,且
地,且![]() 地运往
地运往![]() 地不超过12立方米,则
地不超过12立方米,则![]() 、
、![]() 两地运往
两地运往![]() 、
、![]() 两地哪几种方案?
两地哪几种方案?
(3)已知从![]() 、
、![]() 、
、![]() 三地把垃圾运往
三地把垃圾运往![]() 、
、![]() 两地处理所需费用如下表:
两地处理所需费用如下表:
|
|
| |
运往 | 22 | 20 | 20 |
运往 | 20 | 22 | 21 |
在(2)的条件下,请说明哪种方案的总费用最少?