题目内容
【题目】如图,抛物线y=-x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D,C关于抛物线的对称轴对称,直线AD与y轴相交于点E.
(1)求直线AD的解析式;
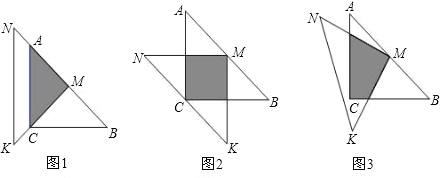
(2)如图1,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH周长的最大值;
(3)如图2,点M是抛物线的顶点,点P是y轴上一动点,点Q是坐标平面内一点,四边形APQM是以PM为对角线的平行四边形,点Q′与点Q关于直线AM对称,连接M Q′,P Q′.当△PM Q′与□APQM重合部分的面积是□APQM面积的![]() 时,求□APQM面积.
时,求□APQM面积.

【答案】(1)直线AD的解析式为:y=x+1;
(2)△FGH周长的最大值为![]() ;
;
(3)□APQM面积为5或10.
【解析】试题分析:(1)根据抛物线解析式求得点A、B、C点坐标,由点D,C关于抛物线的对称轴对称得点D坐标,继而利用待定系数法求解可得;
(2)设点F(x,-x2+2x+3),根据FH∥x轴及直线AD的解析式y=x+1可得点H(-x2+2x+2,-x2+2x+3),继而表示出FH的长度,根据二次函数的性质可得FH的最值情况,易得△FGH为等腰直角三角形,从而可得其周长的最大值;
(3)设P(0,p),根据平行四边形性质及点M坐标可得Q(2,4+p),分P点在AM下方与P点在AM上方两种情况,根据重合部分的面积关系及对称性求得点P的坐标后即可得APQM面积.
试题解析:(1)令-x2+2x+3=0,
解得x1=-1,x2=3,
∴A(-1,0),C(0,3),
∵点D,C关于抛物线的对称轴对称,
∴D(2,3),
∴直线AD的解析式为:y=x+1;
(2)设点F(x,-x2+2x+3),
∵FH∥x轴,
∴H(-x2+2x+2,-x2+2x+3),
∴FH=-x2+2x+2-x=-(x-![]() )2+
)2+![]() ,
,
∴FH的最大值为![]() ,
,
由直线AD的解析式为:y=x+1可知∠DAB=45°,
∵FH∥AB,
∴∠FHG=∠DAB=45°,
∴FG=GH=![]() ×
×![]() =
=![]()
故△FGH周长的最大值为![]() ×2+
×2+![]() =
=![]() ;
;
(3)①当P点在AM下方时,如图,
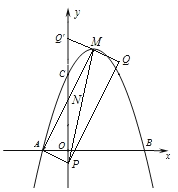
设P(0,p),易知M(1,4),从而Q(2,4+p),
∵△PM Q′与□APQM重合部分的面积是□APQM面积的![]() ,
,
∴PQ′必过AM中点N(0,2),
∴可知Q′在y轴上,易知QQ′的中点T的横坐标为1,而点T必在直线AM上,
故T(1,4),从而T、M重合,
故□APQM是矩形,
易得直线AM解析式为:y=2x+2,
∴直线QQ′:y=-![]() x+
x+![]() ,
,
∴4+p=-![]() ×2+
×2+![]() ,∴p=-
,∴p=-![]() ,(注:此处也可用AM2+AP2=MP2得出p=-
,(注:此处也可用AM2+AP2=MP2得出p=-![]() ),∴PN=
),∴PN=![]() ,
,
∴S□APQM=2S△AMP=4S△ANP=4×![]() ×PN×AO=4×
×PN×AO=4×![]() ×
×![]() ×1=5;
×1=5;
②当P点在AM上方时,如图,

设P(0,p),易知M(1,4),从而Q(2,4+p),
∵△PM Q′与□APQM重合部分的面积是□APQM面积的![]() ,
,
∴PQ′必过QM中点R(![]() ,4+
,4+![]() ),
),
易得直线QQ′:y=-![]() x+p+5,
x+p+5,
联立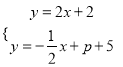 解得:x=
解得:x=![]() ,y=
,y=![]() ,
,
∴H(![]() ,
, ![]() ),
),
∵H为QQ′中点,故易得Q′(![]() ,
, ![]() ),
),
由P(0,p)、R(![]() ,4+
,4+![]() )易得直线PR解析式为:y=(
)易得直线PR解析式为:y=(![]() -
-![]() )x+p,
)x+p,
将Q′(![]() ,
, ![]() )代入到y=(
)代入到y=(![]() -
-![]() )x+p得:
)x+p得:
![]() =(
=(![]() -
-![]() )×
)×![]() +p,
+p,
整理得:p2-9p+14=0,解得p1=7,p2=2(与AM中点N重合,舍去),
∴P(0,7),∴PN=5,
∴S□APQM=2S△AMP=2×![]() ×PN×∣xM -xA∣=2×
×PN×∣xM -xA∣=2×![]() ×5×2=10.
×5×2=10.
综上所述,□APQM面积为5或10

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案