题目内容
【题目】已知有9张卡片,分别写有1到9这就个数字,将它们的背面朝上洗匀后,任意抽出一张,记卡片上的数字为a,若数a使关于x的不等式组 有解,且使函数
有解,且使函数![]() 在x≥7的范围内y随着x的增大而增大,则这9个数中满足条件的a的值的和是( )
在x≥7的范围内y随着x的增大而增大,则这9个数中满足条件的a的值的和是( )
A. 10 B. 11 C. 12 D. 13
【答案】D
【解析】解:解不等式4x≥3(x+1),可得:x≥3,解不等式2x﹣![]() <a,可得:x<
<a,可得:x<![]() .∵不等式组
.∵不等式组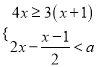 有解,∴
有解,∴![]() >3,解得a>5.∵y=x2﹣2ax=(x﹣a)2﹣a2,∴对称轴为x=a,开口向上,∴当x≥a时,y随x的增大而增大.∵函数y=x2﹣2ax在x≥7的范围内y随x增大而增大,∴a≤7,综上可知5<a≤7.∵a为1到9这九个数字中的一个,∴a的值为6或7,∴满足条件的a的值之和=6+7=13.故选D.
>3,解得a>5.∵y=x2﹣2ax=(x﹣a)2﹣a2,∴对称轴为x=a,开口向上,∴当x≥a时,y随x的增大而增大.∵函数y=x2﹣2ax在x≥7的范围内y随x增大而增大,∴a≤7,综上可知5<a≤7.∵a为1到9这九个数字中的一个,∴a的值为6或7,∴满足条件的a的值之和=6+7=13.故选D.

练习册系列答案
相关题目
【题目】莒南县欲从某师范院校招聘一名“特岗教师”,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:
候选人 | 甲 | 乙 | 丙 | 丁 | |
测试成绩 | 面试 | 86 | 91 | 90 | 83 |
笔试 | 90 | 83 | 83 | 92 | |
根据录用程序,作为人民教师面试的成绩应该比笔试的成绩更重要,并分别赋予它们6和4的权.根据四人各自的平均成绩,你认为将录取( )
A.甲B.乙C.丙D.丁
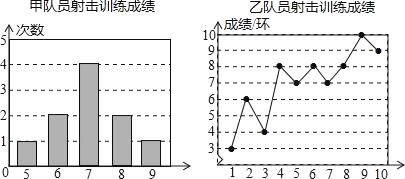
【题目】甲、乙两名队员参加射击训练(各射击10次),成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下表:
平均成绩/环 | 中位数/环 | 众数/环 | 方差/环2 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)求出表格中a,b,c的值;
(2)分别运用表中的统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?