��Ŀ����
����Ŀ����üɽ�п�չ�����ۺ������Ļ�У���Ҫ��![]() ��
��![]() ��
��![]() ���ص�����50�����ס�40�����ס�50������ȫ����������������
���ص�����50�����ס�40�����ס�50������ȫ����������������![]() ��
��![]() ���ؽ��д�������֪����
���ؽ��д�������֪����![]() �ص�����������
�ص�����������![]() �ص�������2����10�����ף�
�ص�������2����10�����ף�
��1�����������ص��������Ƕ��������ף�
��2����![]() ������
������![]() ��
��![]() ������
������![]() ��������
��������![]() ������
������![]() ��30�����ף�
��30�����ף�![]() ������
������![]() �ص�����С��
�ص�����С��![]() ������
������![]() �ص�2��������ȫ������
�ص�2��������ȫ������![]() �أ���
�أ���![]() ������
������![]() �ز�����12�����ף���
�ز�����12�����ף���![]() ��
��![]() ��������
��������![]() ��
��![]() �����ļ��ַ�����
�����ļ��ַ�����
��3����֪��![]() ��
��![]() ��
��![]() ���ذ���������
���ذ���������![]() ��
��![]() ���ش�������������±���
���ش�������������±���
|
|
| |
���� | 22 | 20 | 20 |
���� | 20 | 22 | 21 |
�ڣ�2���������£���˵�����ַ������ܷ������٣�
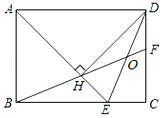
���𰸡���1��������D��90�����ף�����E��50�����ף���2������������3����һ�ַ������ܷ������٣�
��������
��1��������E��x�����ף���������г�����x�ķ��̣����x��ֵ���ɣ�
��2���������г�����a��һԪһ�β���ʽ�飬���a��ȡֵ��Χ���ٸ���a�������ɵó�a��ֵ������������𰸣�
��3�����ݣ�1���е����ַ����������ü��ɣ�
��1��������E��x�����ף�������ã�x+2x-10=140��
��ã�x=50��
��2x-10=90��
�𣺹�����D��90�����ף�����E��50�����ף�
��2��������ɵã�
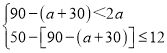 ��
��
��ã�20��a��22��
��a��������
��a=21��22��
�����������ַ�����
��һ�֣�A������D��21�����ף�����E��29�����ף�
C������D��39�����ף�����E��11�����ף�
�ڶ��֣�A������D��22�����ף�����E��28�����ף�
C������D��38�����ף�����E��12�����ף�
��3����һ�ַ���������ã�
22��21+20��29+30��20+22��10+39��20+11��21=2873��Ԫ����
�ڶ��ַ���������ã�
22��22+28��20+30��20+22��10+38��20+12��21=2876��Ԫ����
���ԣ���һ�ַ������ܷ������٣�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ������������ijʦ��ԺУ��Ƹһ�����ظڽ�ʦ�����Լס��ҡ���������λ��ѡ�˽��������Ժͱ��ԣ����ǵijɼ������
��ѡ�� | �� | �� | �� | �� | |
���Գɼ� | ���� | 86 | 91 | 90 | 83 |
���� | 90 | 83 | 83 | 92 | |
����¼�ó�����Ϊ�����ʦ���Եijɼ�Ӧ�ñȱ��Եijɼ�����Ҫ�����ֱ�������6��4��Ȩ.�������˸��Ե�ƽ���ɼ�������Ϊ��¼ȡ�� ��
A.��B.��C.��D.��