题目内容
如图, 在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程
在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程 的两个根,且OA>OB.
的两个根,且OA>OB.

(1)求sin∠ABC的值.
(2)若E为x轴上的点,且 ,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?
,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?
(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,请直接写出F点的坐标;若不存在,请说明理由.
 在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程
在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程 的两个根,且OA>OB.
的两个根,且OA>OB.
(1)求sin∠ABC的值.
(2)若E为x轴上的点,且
 ,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?
,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,请直接写出F点的坐标;若不存在,请说明理由.
(1)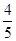 (2)
(2)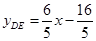 ,yDE=
,yDE= 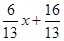 △AOE∽△DAO(3)F1 (3 , 8) ; F2 (-3 , 0) ; F3 (
△AOE∽△DAO(3)F1 (3 , 8) ; F2 (-3 , 0) ; F3 (
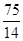 ,
,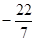 ); F4(-
); F4(-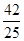 ,
,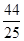 )
)
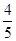 (2)
(2)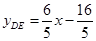 ,yDE=
,yDE= 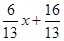 △AOE∽△DAO(3)F1 (3 , 8) ; F2 (-3 , 0) ; F3 (
△AOE∽△DAO(3)F1 (3 , 8) ; F2 (-3 , 0) ; F3 (
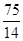 ,
,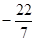 ); F4(-
); F4(-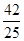 ,
,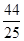 )
)解:(1) 解x2-7x+12=0得x1=4,x2=3
∵OA>OB
∴OA =4, OB=3 ·························· 1分
在Rt△AOB中,由勾股定理有AB=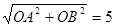
∴sin∠ABC=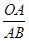 =
=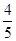 ······················· 1分
······················· 1分
(2)∵点E在x轴上,S△AOE=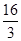 有
有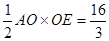
得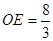 ∴E(
∴E(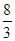 ,0)或E(—
,0)或E(—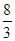 ,0)················· 1分
,0)················· 1分
由已知可知D(6,4) 设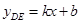 ,
,
当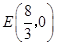 时有
时有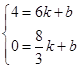
解得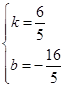
∴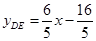 ···························· 1分
···························· 1分
同理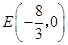 时,yDE=
时,yDE= 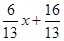 ·················· 1分
·················· 1分
在△AOE中,∠AOE=90°,OA=4,OE=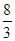
在△AOD中,∠OAD=90°,OA=4,OD=6
∵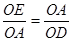
∴△AOE∽△DAO ······················· 1分
(3)满足条件的点有四个
F1 (3 , 8) ; F2 (-3 , 0) ; F3 (
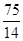 ,
,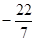 ); F4(-
); F4(-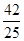 ,
,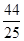 )
)
······································ 4分
说明:本卷中所有题目,若由其它方法得出正确结论,可参照本评分标准酌情给分.
(1)解一元二次方程求出OA,OB的长度,再利用勾股定理求出AB的长度,再代入计算即可;
(2)先根据三角形的面积求出点E的坐标,并根据平行四边形的对边相等的性质求出点D的坐标,然后利用待定系数法求解直线的解析式;分别求出两三角形夹直角的两对应边的比,如果相等,则两三角形相似,否则不相似;
(3)根据菱形的性质,分AC与AF是邻边并且点F在射线AB上与射线BA上两种情况,以及AC与AF分别是对角线的情况分别进行求解计算.
∵OA>OB
∴OA =4, OB=3 ·························· 1分
在Rt△AOB中,由勾股定理有AB=
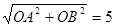
∴sin∠ABC=
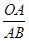 =
=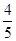 ······················· 1分
······················· 1分(2)∵点E在x轴上,S△AOE=
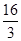 有
有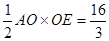
得
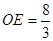 ∴E(
∴E(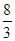 ,0)或E(—
,0)或E(—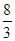 ,0)················· 1分
,0)················· 1分由已知可知D(6,4) 设
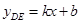 ,
, 当
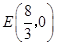 时有
时有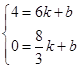
解得
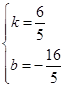
∴
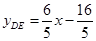 ···························· 1分
···························· 1分同理
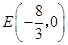 时,yDE=
时,yDE= 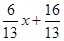 ·················· 1分
·················· 1分在△AOE中,∠AOE=90°,OA=4,OE=
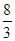
在△AOD中,∠OAD=90°,OA=4,OD=6
∵
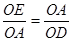
∴△AOE∽△DAO ······················· 1分
(3)满足条件的点有四个
F1 (3 , 8) ; F2 (-3 , 0) ; F3 (

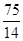 ,
,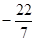 ); F4(-
); F4(-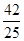 ,
,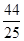 )
)······································ 4分
说明:本卷中所有题目,若由其它方法得出正确结论,可参照本评分标准酌情给分.
(1)解一元二次方程求出OA,OB的长度,再利用勾股定理求出AB的长度,再代入计算即可;
(2)先根据三角形的面积求出点E的坐标,并根据平行四边形的对边相等的性质求出点D的坐标,然后利用待定系数法求解直线的解析式;分别求出两三角形夹直角的两对应边的比,如果相等,则两三角形相似,否则不相似;
(3)根据菱形的性质,分AC与AF是邻边并且点F在射线AB上与射线BA上两种情况,以及AC与AF分别是对角线的情况分别进行求解计算.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
 地出发向
地出发向 地行走,同时晓阳从
地行走,同时晓阳从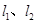 分别表示小明、晓阳离A地的距离
分别表示小明、晓阳离A地的距离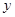 (千米)与已用时间
(千米)与已用时间 (分钟)之间的关系,
(分钟)之间的关系,

 )本。
)本。 的图象与y轴交于点
的图象与y轴交于点 ,且与两坐标轴围成的三角形面积是20,求该一次函数的解析式。
,且与两坐标轴围成的三角形面积是20,求该一次函数的解析式。
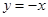 ,直线
,直线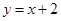 与
与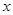 轴围成图形的周长是 (结果保留根号).
轴围成图形的周长是 (结果保留根号).