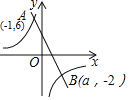题目内容
【题目】在平面直角坐标系中，点O为原点，点A的坐标为（﹣8，0）．如图1，正方形OBCD的顶点B在x轴的负半轴上，点C在第二象限．现将正方形OBCD绕点O顺时针旋转角α得到正方形OEFG．
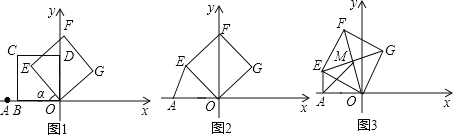
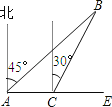
（1）如图2，若α＝45°，OE＝OA，求直线EF的函数表达式；
（2）如图3，若α为锐角，且tanα＝
，当EA⊥x轴时，正方形对角线EG与OF相交于点M，求线段AM的长；
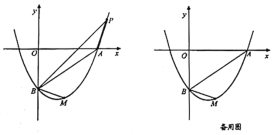
（3）当正方形OEFG的顶点F落在y轴正半轴上时，直线AE与直线FG相交于点P，是否存在△OEP的两边之比为
：1？若存在，求出点P的坐标；若不存在，试说明理由．
【答案】(1)直线EF的解析式为y＝x+8
；(2)AM＝6；(3)满足条件的点P的坐标为(0，8)，(﹣8，24)，(﹣24，48)．
【解析】
(1)过点E作EH⊥OA于点H,进而求出点E的坐标,再根据勾股定理求出OF的值,然后利用待定系数法,即可求出直线EF的解析式
(2)作MN⊥AM交x轴于点N,此时△AEM≌△NOM,得到AE=ON=4,△AMN是等腰直角三角形,即可求出AM的长;
(3)根据点F落在y轴正半轴上,通过改变正方形的边长,画出直线AE与直线FG相交的点P,并判断△OEP的其中两边之比能否为2:1,当△OEP的其中两边之比为 :1时,再通过分类讨论确定出图形,根据图形性质,利用勾股定理、相似三角形、三角函数等知识求得点P的坐标
(1)∵OE＝OA＝8，α＝45°，
∴E(﹣4，4)，F(0，8)，
设直线EF的解析式为y＝kx+b，则有
，
解得
∴直线EF的解析式为y＝x+8．
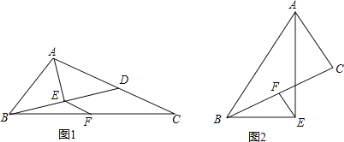
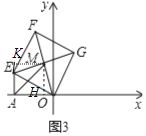
(2)如图3中，作MH⊥OA于H，MK⊥AE交AE的延长线于K．
在Rt△AEO中，tan∠AOE＝
，OA＝8，
∴AE＝4，
∵四边形EOGF是正方形，
∴∠EMO＝90°，
∵∠EAO＝∠EMO＝90°，
∴E、A、O、M四点共圆，
∴∠EAM＝∠EOM＝45°，
∴∠MAK＝∠MAH＝45°，∵MK⊥AE，MH⊥OA，
∴MK＝MH，四边形KAOM是正方形，
∵EM＝OM，
∴△MKE≌△MHO，
∴EK＝OH，
∴AK+AH＝2AH＝AE+EK+OA﹣OH＝12，
∴AH＝6，
∴AM＝AH＝6．
(3)如图2中，设F(0，2a)，则E(﹣a，a)．
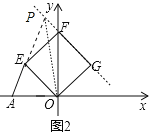
∵A(﹣8，0)，E(﹣a，a)，
∴直线AP的解析式为y＝
，直线FG的解析式为y＝﹣x+2a，
由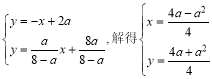
，
∴P(
)．
①当PO＝ OE时，∴PO2＝2OE2，
则有：
＝4a2，
解得a＝4或﹣4(舍弃)或0(舍弃)，
此时P(0，8)．
②当PO＝PE时，则有：＝2[(
)2]，
解得：a＝4或12，
此时P(0，8)或(﹣24，48)，
③当PE＝EO时，[()2]＝4a2，
解得a＝8或0(舍弃)，
∴P(﹣8，24)
综上所述，满足条件的点P的坐标为(0，8)，(﹣8，24)，(﹣24，48)．
